题目内容
3.计算:(1)(x2•xm)÷x2m;
(2)(-1)999×(-2)1000×0.51000;
(3)($\frac{1}{2}$)99×1625;
(4)4-(-2)-2-32÷(-3)0.
分析 (1)利用同底数幂的乘除法的计算方法计算;
(2)利用积的乘方计算即可;
(3)利用幂的乘方和积的乘方计算;
(1)先算乘方、负指数幂和0指数幂,再算除法,最后算减法.
解答 解:(1)原式=(xm+2÷x2m
=x2-m;
(2)原式=(-1)×(2×0.5)1000
=-1×1
=-1;
(3)原式=($\frac{1}{2}$)99×2100;
=($\frac{1}{2}$×2)99×2
=2;
(4)原式=4-$\frac{1}{4}$-9÷1
=-5$\frac{1}{4}$.
点评 此题考查整式的混合运算,掌握计算方法和运算的顺序是解决问题的关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
14. 如图,AD、BE是△ABC的中线,则下列结论中,正确的个数有( )
如图,AD、BE是△ABC的中线,则下列结论中,正确的个数有( )
(1)S△AOE=S△COE; (2)S△AOB=S四边形EODC;
(3)S△BOC=2S△COE; (4)S△ABC=4S△BOC.
 如图,AD、BE是△ABC的中线,则下列结论中,正确的个数有( )
如图,AD、BE是△ABC的中线,则下列结论中,正确的个数有( )(1)S△AOE=S△COE; (2)S△AOB=S四边形EODC;
(3)S△BOC=2S△COE; (4)S△ABC=4S△BOC.
| A. | .1个 | B. | .2个 | C. | .3个 | D. | .4个 |
11.3月15日是国际消费者权益日.某品牌专卖店准备出售甲、乙两种服装.其中甲、乙两种服装的进价和售价如表:
已知:专卖店用3000元购进甲种服装的数量与用2400元购进乙种服装的数量相同.
(1)求m的值;
(2)要使购进的甲、乙两种服装共200件的总利润(利润=售价-进价)不少于21700元,且甲种服装的件数不超过总件数的一半,问该专卖店有几种进货方案?
(3)在(2)的条件下,专卖店准备对甲种服装进行优惠促销活动,决定对甲种服装每件优惠a(50<a<70)元出售,乙种服装价格不变.那么该专卖店要获得最大利润应如何进货?
| 服装价格 | 甲 | 乙 |
| 进价(元/件) | m | m-20 |
| 售价(元/件) | 240 | 160 |
(1)求m的值;
(2)要使购进的甲、乙两种服装共200件的总利润(利润=售价-进价)不少于21700元,且甲种服装的件数不超过总件数的一半,问该专卖店有几种进货方案?
(3)在(2)的条件下,专卖店准备对甲种服装进行优惠促销活动,决定对甲种服装每件优惠a(50<a<70)元出售,乙种服装价格不变.那么该专卖店要获得最大利润应如何进货?
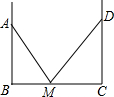 如图,装修师傅装修一间房子,在两墙之间有一个底端在点M的梯子,当它靠在一侧墙上时,梯子的顶端在点A,当它靠在另一侧墙上时,梯子的顶端在点D,已知∠AMB=55°,∠DMC=44°,点A到地面的垂直距离为4m,求点D到地面垂直的距离.(参考数据:sin55°≈0.8192,sin44°≈0.6947)
如图,装修师傅装修一间房子,在两墙之间有一个底端在点M的梯子,当它靠在一侧墙上时,梯子的顶端在点A,当它靠在另一侧墙上时,梯子的顶端在点D,已知∠AMB=55°,∠DMC=44°,点A到地面的垂直距离为4m,求点D到地面垂直的距离.(参考数据:sin55°≈0.8192,sin44°≈0.6947) 如图,在△ABC中,∠C=60°,且高BE经过高AD的中点F.求证:BF=4EF.
如图,在△ABC中,∠C=60°,且高BE经过高AD的中点F.求证:BF=4EF. 某校为培育青少年科技创新能力,举办了动漫制作活动,小华设计了点沿线段往返运动的一个雏形,甲以3cm/s的速度从A出发到B在返回到A,同时乙以每小时4cm/s的速度从B出发到A在返回到B.A,B的距离为21cm.
某校为培育青少年科技创新能力,举办了动漫制作活动,小华设计了点沿线段往返运动的一个雏形,甲以3cm/s的速度从A出发到B在返回到A,同时乙以每小时4cm/s的速度从B出发到A在返回到B.A,B的距离为21cm.