题目内容
8. 如图,在△ABC中,∠C=60°,且高BE经过高AD的中点F.求证:BF=4EF.
如图,在△ABC中,∠C=60°,且高BE经过高AD的中点F.求证:BF=4EF.
分析 由AD⊥BC于点D,可得∠ADC=90°,由∠C=60°,得出∠CAD=30°,那么在直角△AEF中,由∠EAF=30°,可得:AF=2EF,然后由AF=DF,可得DF=2EF,再求出∠FBD=30°,进而可得BF=2FD=4EF.
解答 证明:∵AD⊥BC于点D,
∴∠ADC=90°,
∵∠C=60°,
∴∠CAD=30°,
∵BE⊥AC于点E,
∴∠AEF=90°,
∵∠EAF=30°,
∴AF=2EF,
∵AF=DF,
∴DF=2EF, ∵AD⊥BC于点D,
∵AD⊥BC于点D,
∴∠BDF=90°,
∵∠AFE=∠BFD,且∠EAD+∠AFE+∠AEF=∠FBD+∠BDF+∠BFD=180°,
∴∠FBD=30°,
∴BF=2FD=4EF,
即BF=4EF.
点评 此题考查了含30°角的直角三角形的性质,熟记30°角所对的直角边等于斜边的一半,是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
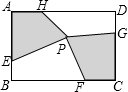 如图,在矩形SBCD中,点E、F、H分别在边AB、BC、CD、DA上,点P在矩形ABCD内,若AB=6,BC=8,AE=CG=4,BF=DH=6,四边形AEPH的面积为11,则四边形PFCG的面积为11.
如图,在矩形SBCD中,点E、F、H分别在边AB、BC、CD、DA上,点P在矩形ABCD内,若AB=6,BC=8,AE=CG=4,BF=DH=6,四边形AEPH的面积为11,则四边形PFCG的面积为11.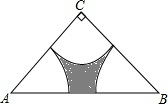 如图,在Rt△ABC中,∠C=90°,CA=CB=4,分别以A、B、C为圆心,以$\frac{1}{2}$AC为半径画弧,求三条弧与边AB所围成的阴影部分的面积.
如图,在Rt△ABC中,∠C=90°,CA=CB=4,分别以A、B、C为圆心,以$\frac{1}{2}$AC为半径画弧,求三条弧与边AB所围成的阴影部分的面积.