题目内容
6．
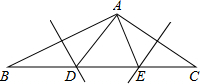如图，在△ABC中，已知AB，AC的垂直平分线分别交BC于点D，E，且∠BAC=125°，则∠DAE是70度．
分析 由∠BAC=125°，利用三角形的内角和定理，可求得∠B+∠C的度数，又由AB，AC的垂直平分线分别交BC于点D，E，根据线段垂直平分线的性质，可得AD=BD，AE=CE，继而可得∠BAD=∠B，∠CAE=∠C，则可求得∠BAD+∠CAE的度数，继而求得答案．
解答 解：∵∠BAC=125°，
∴∠B+∠C=55°，
∵AB，AC的垂直平分线分别交BC于点D，E，
∴AD=BD，AE=CE，
∴∠BAD=∠B，∠CAE=∠C，
∴∠BAD+∠CAE=∠B+∠C=55°，
∴∠DAE=∠BAC-（∠B+∠C）=70°．
故答案为：70．
点评 此题考查了线段垂直平分线的性质以及等腰三角形的性质．注意垂直平分线上任意一点，到线段两端点的距离相等．
练习册系列答案
相关题目
17．
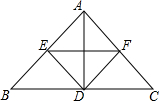如图，在△ABC中，AB⊥AC，AD⊥BC，点D是BC的中点，DE⊥AB，DF⊥AC，连接EF，则图中等腰直角三角形的个数是（ ）
如图，在△ABC中，AB⊥AC，AD⊥BC，点D是BC的中点，DE⊥AB，DF⊥AC，连接EF，则图中等腰直角三角形的个数是（ ）| A． | 8个 | B． | 10个 | C． | 12个 | D． | 13个 |
如图，△ABC和△CDE是两个不全等的等边三角形．AC、AD分别交BE与G、F点，AD与CE交于H点．猜想：
如图，在平行四边形ABCD中，E为BF延长线上一点，求证：$\frac{BO}{FO}$=$\frac{EO}{BO}$．