题目内容
2.作函数y=-x2的图象,并根据图象回答问题.(1)列表:
| x | … | -3 | 0 | 1 | 2 | … | |||
| y=-x2 | … | -4 | -1 | -9 | … |
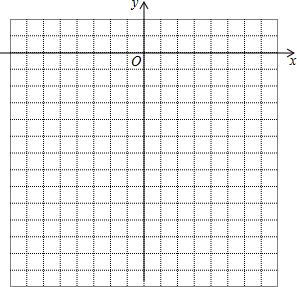
(3)函数y=-x2的图象是一条抛物线,开口向下,对称轴为y(x或y)轴,顶点坐标是(0,0),函数有最大(大或小)值0.
(4)在函数y=-x2中,当x>0时,若x1>x2,函数值y1<y2;当x<0时,若x1>x2,函数值y1>y2.
分析 (1)画出函数图象,根据函数图象填表即可;
(2)在坐标系内描出各点,画出函数图象即可;
(3)(4)根据函数图象即可得出结论.
解答 解:(1)如图,
| x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y=-x2 | … | -9 | -4 | -1 | 0 | -1 | -4 | -9 | … |

(3)由图可知,函数y=-x2的图象是一条抛物线,开口向下,对称轴为y(x或y)轴,顶点坐标是(0,0),函数有最大(大或小)值.
故答案为:抛物,下,y,(0,0),大,0;
(4)由函数图象可知,在函数y=-x2中,当x>0时,若x1>x2,函数值y1<y2;当x<0时,若x1>x2,函数值y1>y2.
故答案为:<,>.
点评 本题考查的是二次函数的图象,能利用描点法函数函数图象,利用数形结合求解是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.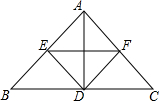 如图,在△ABC中,AB⊥AC,AD⊥BC,点D是BC的中点,DE⊥AB,DF⊥AC,连接EF,则图中等腰直角三角形的个数是( )
如图,在△ABC中,AB⊥AC,AD⊥BC,点D是BC的中点,DE⊥AB,DF⊥AC,连接EF,则图中等腰直角三角形的个数是( )
 如图,在△ABC中,AB⊥AC,AD⊥BC,点D是BC的中点,DE⊥AB,DF⊥AC,连接EF,则图中等腰直角三角形的个数是( )
如图,在△ABC中,AB⊥AC,AD⊥BC,点D是BC的中点,DE⊥AB,DF⊥AC,连接EF,则图中等腰直角三角形的个数是( )| A. | 8个 | B. | 10个 | C. | 12个 | D. | 13个 |
 已知如图,△ABC是等边三角形,DE∥BC,交AB、AC于D、E,试说明△ADE是等边三角形.
已知如图,△ABC是等边三角形,DE∥BC,交AB、AC于D、E,试说明△ADE是等边三角形.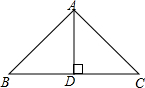 如图是小磊制作的一个三角形钢架模型ABC,其中BC=xcm,且BC+AD=40cm,设△ABC的面积为Scm2
如图是小磊制作的一个三角形钢架模型ABC,其中BC=xcm,且BC+AD=40cm,设△ABC的面积为Scm2 如图,△ABC和△CDE是两个不全等的等边三角形.AC、AD分别交BE与G、F点,AD与CE交于H点.猜想:
如图,△ABC和△CDE是两个不全等的等边三角形.AC、AD分别交BE与G、F点,AD与CE交于H点.猜想: 如图,在平行四边形ABCD中,E为BF延长线上一点,求证:$\frac{BO}{FO}$=$\frac{EO}{BO}$.
如图,在平行四边形ABCD中,E为BF延长线上一点,求证:$\frac{BO}{FO}$=$\frac{EO}{BO}$.