题目内容
9. 如图,某居民小区要在一块一边靠墙(墙长20m)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长为50m的栅栏围成,设花园的BC边长为x(m),花园的面积为S(m2).
如图,某居民小区要在一块一边靠墙(墙长20m)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长为50m的栅栏围成,设花园的BC边长为x(m),花园的面积为S(m2).(1)求S与x之间的函数解析式,并写出自变量x的取值范围;
(2)当边长BC为多少米时,花园的面积最大,最大面积是多少?
分析 (1)首先根据矩形的性质,由花园的BC边长为x(m),可得AB=$\frac{50-x}{2}$,然后根据矩形面积的求解方法,即可求得S与x之间的函数关系式,又由墙长20m,即可求得自变量x的范围;
(2)根据(1)中的二次函数的增减性,可知当x<25时,S随x的增大而增大,故可得当x=20时,S最大,将其代入函数解析式,即可求得最大面积.
解答 解:(1)∵四边形ABCD是矩形,
∴AB=CD,AD=BC,
∵BC=xm,AB+BC+CD=50m,
∴AB=$\frac{50-x}{2}$,
∴花园的面积为:S=x•$\frac{50-x}{2}$=-$\frac{1}{2}$x2+25x(0<x≤20);
∴S与x之间的函数关系式为:S=-$\frac{1}{2}$x2+25x(0<x≤20);
(2)∵S=-$\frac{1}{2}$x2+25x=-$\frac{1}{2}$(x-25)2+312.5,
∵a=-$\frac{1}{2}$<0,
∴当x<25时,y随x的增大而增大,
∴当x=20时,y最大,最大值y=300m2.
∴当x=20m时,花园的面积最大,最大面积为300m2.
点评 此题考查了二次函数的实际应用问题.此题难度较大,解题的关键是理解题意,能根据题意求得函数解析式,然后根据二次函数的性质求解.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
17.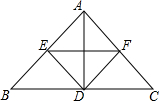 如图,在△ABC中,AB⊥AC,AD⊥BC,点D是BC的中点,DE⊥AB,DF⊥AC,连接EF,则图中等腰直角三角形的个数是( )
如图,在△ABC中,AB⊥AC,AD⊥BC,点D是BC的中点,DE⊥AB,DF⊥AC,连接EF,则图中等腰直角三角形的个数是( )
 如图,在△ABC中,AB⊥AC,AD⊥BC,点D是BC的中点,DE⊥AB,DF⊥AC,连接EF,则图中等腰直角三角形的个数是( )
如图,在△ABC中,AB⊥AC,AD⊥BC,点D是BC的中点,DE⊥AB,DF⊥AC,连接EF,则图中等腰直角三角形的个数是( )| A. | 8个 | B. | 10个 | C. | 12个 | D. | 13个 |
 设有理数a,b,c在数轴上的对应点如图所示,|a|<|c|,化简|b-a|+|a+c|+|c-b|.
设有理数a,b,c在数轴上的对应点如图所示,|a|<|c|,化简|b-a|+|a+c|+|c-b|. 如图,△ABC和△CDE是两个不全等的等边三角形.AC、AD分别交BE与G、F点,AD与CE交于H点.猜想:
如图,△ABC和△CDE是两个不全等的等边三角形.AC、AD分别交BE与G、F点,AD与CE交于H点.猜想: