题目内容
7.观察下列各式:1${\;}^{2}+{2}^{2}=\frac{1}{6}×2×3×5$
12+22+32=$\frac{1}{6}×3×4×7$
12+22+32+42=$\frac{1}{6}×4×5×9$,…
①由此推算出12+22+32+…+102等于多少?
②12+22+32+…+n2等于多少?
分析 由题意可知:从1开始连续自然数的平方和等于最后一个自然数乘这个数加1,再乘这个数的2倍加1,最后乘$\frac{1}{6}$得出结果,由此规律计算得出答案即可.
解答 解:①12+22+32+…+102=$\frac{1}{6}$×10×(10+1)(2×10+1)=385;
②12+22+32+…+n2=$\frac{1}{6}$n(n+1)(2n+1).
点评 此题考查数字的变化规律,发现数字之间的联系,找出数字之间的运算规律,利用规律解决问题.

练习册系列答案
相关题目
17.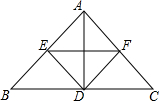 如图,在△ABC中,AB⊥AC,AD⊥BC,点D是BC的中点,DE⊥AB,DF⊥AC,连接EF,则图中等腰直角三角形的个数是( )
如图,在△ABC中,AB⊥AC,AD⊥BC,点D是BC的中点,DE⊥AB,DF⊥AC,连接EF,则图中等腰直角三角形的个数是( )
 如图,在△ABC中,AB⊥AC,AD⊥BC,点D是BC的中点,DE⊥AB,DF⊥AC,连接EF,则图中等腰直角三角形的个数是( )
如图,在△ABC中,AB⊥AC,AD⊥BC,点D是BC的中点,DE⊥AB,DF⊥AC,连接EF,则图中等腰直角三角形的个数是( )| A. | 8个 | B. | 10个 | C. | 12个 | D. | 13个 |
17.下列说法中错误的是( )
| A. | 一个正数的绝对值一定是正数 | |
| B. | 一个负数的绝对值一定是正数 | |
| C. | 离原点3个单位长度的点表示的数的绝对值是3 | |
| D. | 如果a是非正数,那么a的绝对值比它本身大 |