题目内容
8．
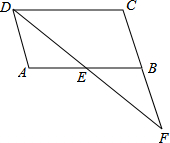如图，在?ABCD中，点E是AB边的中点，DE的延长线与CB的延长线交于点F．求证：BC=BF．
分析 首先由平行四边形的性质可得AD=BC，再由全等三角形的判定定理AAS可证明△ADE≌△BFE由此可得AD=BF，进而可证明BC=BF．
解答 证明：∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC，
又∵点F在CB的延长线上，
∴AD∥CF，
∴∠1=∠2．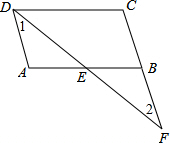
∵点E是AB边的中点，
∴AE=BE．
∵在△ADE与△BFE中，
$\left\{\begin{array}{l}{∠DEA=∠FEB}\\{∠1=∠2}\\{AE=BE}\end{array}\right.$，
∴△ADE≌△BFE（AAS），
∴AD=BF，
∴BC=BF．
点评 本题考查了平行四边形的性质、全等三角形的判定与性质．在应用全等三角形的判定时，要注意三角形间的公共边、对顶角以及公共角．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
如图，△ABC在网格中（每格表示1个单位），如图所示构建平面直角坐标系
19．
如图，A（0，-$\sqrt{2}$），点B为直线y=-x上一动点，当线段AB最短时，点B的坐标为（ ）
如图，A（0，-$\sqrt{2}$），点B为直线y=-x上一动点，当线段AB最短时，点B的坐标为（ ）| A． | （0，0） | B． | （1，-1） | C． | （$\frac{1}{2}$，-$\frac{1}{2}$） | D． | （$\frac{\sqrt{2}}{2}$，-$\frac{\sqrt{2}}{2}$） |
16．在?ABCD中，M为CD的中点．若CD=2AD，则∠AMB的大小为（ ）
| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
“龟兔赛跑”的故事同学们都非常熟悉，图中的线段和折线OABC表示“龟兔赛跑”时路程与时间的关系，请你根据图中给出的信息，下列说法：