题目内容
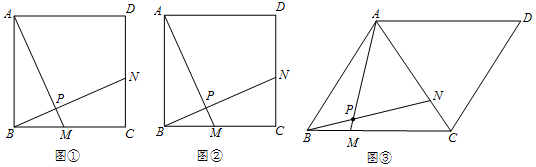
16.在?ABCD中,M为CD的中点.若CD=2AD,则∠AMB的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
分析 由平行四边形的性质,结合已知条件可求得∠MAB+∠MBA=90°,可求得答案.
解答 解:∵四边形ABCD是平行四边形.
∴AB∥CD,AD∥BC,AD=BC,
∴∠DAB+∠ABC=180°,∠MAB=∠DMA,∠MBA=∠BMC,
∵M为CD的中点,如DC=2AD,
∴AD=DM=CM=BC,
∴∠DAM=∠DMA,∠MBC=∠BMC,
∴∠MAB+∠MBA=90°,
∴∠AMB=90°.
故选D.
点评 本题主要考查了平行四边形的性质与等腰梯形的判定与性质,此题有一定的综合性,但难度不大.解题时要注意数形结合思想的应用

练习册系列答案
相关题目


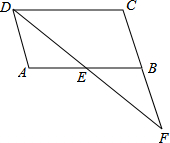 如图,在?ABCD中,点E是AB边的中点,DE的延长线与CB的延长线交于点F.
如图,在?ABCD中,点E是AB边的中点,DE的延长线与CB的延长线交于点F.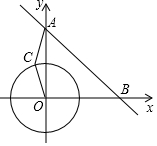 在平面直角坐标系xOy中,已知点A(0,6),点B(6,0),动点C在以半径为2$\sqrt{2}$的⊙O上,连接OC,AC.
在平面直角坐标系xOy中,已知点A(0,6),点B(6,0),动点C在以半径为2$\sqrt{2}$的⊙O上,连接OC,AC.