题目内容
19. 如图,A(0,-$\sqrt{2}$),点B为直线y=-x上一动点,当线段AB最短时,点B的坐标为( )
如图,A(0,-$\sqrt{2}$),点B为直线y=-x上一动点,当线段AB最短时,点B的坐标为( )| A. | (0,0) | B. | (1,-1) | C. | ($\frac{1}{2}$,-$\frac{1}{2}$) | D. | ($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) |
分析 根据A(0,-$\sqrt{2}$),点B为直线y=-x上一动点,可知当AB⊥OB时,线段AB最短,作辅助线BC⊥OA于点C,可得OC=CB,由点A(0,-$\sqrt{2}$),可得点B的坐标,从而本题得以解决.
解答 解:∵A(0,-$\sqrt{2}$),点B为直线y=-x上一动点,
∴当AB⊥OB时,线段AB最短,此时点B在第四象限,作BC⊥OA于点C,∠AOB=45°,如下图所示: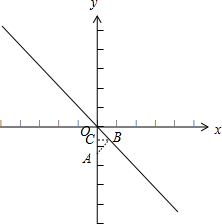
∴OC=CB=$\frac{1}{2}$OA,
∴点B的坐标为($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$).
故选D.
点评 本题考查一次函数图象上点的坐标特征和垂线段最短,解题的关键是明确直线外一点到直线的所有线段中垂线段最短,直线y=-x与两坐标轴的夹角为45°.

练习册系列答案
相关题目
14. 学校开展阳光体育活动,组织九年级学生定点投篮,规定每人投篮3次.现对九年级(5)班每名学生投中篮的次数进行统计,并将统计结果绘制成如下不完整的统计图表.
学校开展阳光体育活动,组织九年级学生定点投篮,规定每人投篮3次.现对九年级(5)班每名学生投中篮的次数进行统计,并将统计结果绘制成如下不完整的统计图表.
根据以上信息,解答下列问题.
(1)补全条形统计图.
(2)被统计学生投中篮的次数的中位数为2.平均数为1.8.
(3)若九年级有学生200人,请估计投中篮的次数在2次以上(包括2次)的人数.
 学校开展阳光体育活动,组织九年级学生定点投篮,规定每人投篮3次.现对九年级(5)班每名学生投中篮的次数进行统计,并将统计结果绘制成如下不完整的统计图表.
学校开展阳光体育活动,组织九年级学生定点投篮,规定每人投篮3次.现对九年级(5)班每名学生投中篮的次数进行统计,并将统计结果绘制成如下不完整的统计图表. | 投中篮的次数(次) | 频数 (人数) | 频率 |
| 0 | 2 | 0.05 |
| 1 | 12 | 0.3 |
| 2 | x | 0.45 |
| 3 | 8 | y |
| 合计 | m | 1 |
(1)补全条形统计图.
(2)被统计学生投中篮的次数的中位数为2.平均数为1.8.
(3)若九年级有学生200人,请估计投中篮的次数在2次以上(包括2次)的人数.
17.点P在∠AOB的平分线上,点P到OA边的距离等于9,点Q是OB边上的任意一点,则下列选项正确的是( )
| A. | PQ≥9 | B. | PQ>9 | C. | PQ<9 | D. | PQ≤9 |

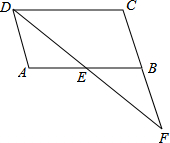 如图,在?ABCD中,点E是AB边的中点,DE的延长线与CB的延长线交于点F.
如图,在?ABCD中,点E是AB边的中点,DE的延长线与CB的延长线交于点F.