题目内容
20.某项工作甲单独做需要4天完成,乙单独做需要6天完成,若乙先做1天,然后再由甲、乙合作完成此项工作,若设甲乙合作需x天完成,则可列的方程为( )| A. | 1+($\frac{1}{4}$+$\frac{1}{6}$)x=1 | B. | $\frac{1}{4}$+($\frac{1}{4}$+$\frac{1}{6}$)x=1 | C. | $\frac{1}{6}$+($\frac{1}{4}$+$\frac{1}{6}$)x=1 | D. | $\frac{1}{6}$+$\frac{(4+6)}{2}$x=1 |
分析 先求出甲、乙的工作效率,再分别求出每部分的工作量,即可得出方程.
解答 解:∵甲单独做需要4天完成,乙单独做需要6天完成,
∴甲的工作效率是$\frac{1}{4}$,乙的工作效率是$\frac{1}{6}$,
∴方程为$\frac{1}{6}$+($\frac{1}{4}$+$\frac{1}{6}$)x=1,
故选C.
点评 本题考查了由实际问题抽象出一元一次方程的应用,能找出相等关系是解此题的关键.

练习册系列答案
相关题目
10. 如图,P是⊙O外一点,PA、PB是⊙O的两条切线,切点分别为A、B,连接AB,OP相交于点C,OP与⊙O相交于点D,则下列结论不正确的是( )
如图,P是⊙O外一点,PA、PB是⊙O的两条切线,切点分别为A、B,连接AB,OP相交于点C,OP与⊙O相交于点D,则下列结论不正确的是( )
 如图,P是⊙O外一点,PA、PB是⊙O的两条切线,切点分别为A、B,连接AB,OP相交于点C,OP与⊙O相交于点D,则下列结论不正确的是( )
如图,P是⊙O外一点,PA、PB是⊙O的两条切线,切点分别为A、B,连接AB,OP相交于点C,OP与⊙O相交于点D,则下列结论不正确的是( )| A. | PA=PB | B. | ∠APO=∠BPO | C. | OC=CD | D. | ∠OAP=90° |
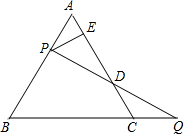 如图,等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上的一点,当PA=CQ时,连接PQ交AC于点D,下列结论:
如图,等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上的一点,当PA=CQ时,连接PQ交AC于点D,下列结论: 如图,在正方形ABCD中,E是CD上一点,F是CB延长线上一点,且DE=BF,AF,AE之间有怎样的关系?请说明理由.
如图,在正方形ABCD中,E是CD上一点,F是CB延长线上一点,且DE=BF,AF,AE之间有怎样的关系?请说明理由.