题目内容
11.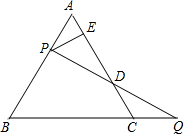 如图,等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上的一点,当PA=CQ时,连接PQ交AC于点D,下列结论:
如图,等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上的一点,当PA=CQ时,连接PQ交AC于点D,下列结论:①PD=DQ;②DE=$\frac{1}{2}$AC;③AE=$\frac{1}{2}$CQ;④PQ⊥AB
其中正确的有①②③.(填序号)
分析 作辅助线PF∥BC,由已知条件可得△APF也是等边三角形,从而可以推出△PFD≌△QCD,从而可得PD与DQ的关系,进而得到DE与AC的关系,AE与CQ的关系,由∠DEP=90°,∠EDP随着点P的变化而变化可以判断PQ与AB的关系.
解答 解:作PF∥BC交AC于点F,如下图所示: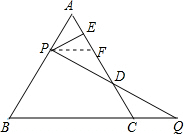
∵△ABC是等边三角形,∠AFP=∠ACB=60°,
∴AP=PF,
∵PA=CQ,
∴FP=CQ,
∵PF∥BC,
∴∠FPD=∠CQD,
在△PFD和△QCD中,
$\left\{\begin{array}{l}{∠FPD=∠CQD}\\{∠PDF=∠QDC}\\{FP=CQ}\end{array}\right.$,
∴△PFD≌△QCD(AAS)
∴PD=QD,(故①正确)DF=DC,
∵△APF是等边三角形,PF⊥AC,
∴AE=EF,
∵DE=DF+EF,AE=EF,DF=CD,AC=AE+EF+FD+DC,
∴DE=$\frac{1}{2}AC$,(故②正确)
∵△APF是等边三角形,PF⊥AC,
∴AE=$\frac{1}{2}AP$,
∵AP=CQ,
∴AE=$\frac{1}{2}CQ$,(故③正确)
∵∠PDA的对边随着点P的变化而变化,而DE的值不变,∠PED=90°不变,∠A=60°不变,
∴∠PDA的正切值在变化,从而∠PDA在变化,
∴∠APD随着点P的变化而变化,
故④不正确.
故答案为:①②③.
点评 本题考查全等三角形的判定与性质、等边三角形的性质,解题的关键由已知条件可以得到各边的关系,然后找出所求问题需要的条件.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
1.一组数据3,-4,6,0,则这组数据的极差是( )
| A. | 10 | B. | 9 | C. | 3 | D. | 2.5 |
2.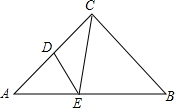 如图,在Rt△ABC中,∠ACB=90°,AC=BC=6,D为AC的中点,E是线段AB边上一动点,连接ED、EC,则△CDE周长的最小值为( )
如图,在Rt△ABC中,∠ACB=90°,AC=BC=6,D为AC的中点,E是线段AB边上一动点,连接ED、EC,则△CDE周长的最小值为( )
 如图,在Rt△ABC中,∠ACB=90°,AC=BC=6,D为AC的中点,E是线段AB边上一动点,连接ED、EC,则△CDE周长的最小值为( )
如图,在Rt△ABC中,∠ACB=90°,AC=BC=6,D为AC的中点,E是线段AB边上一动点,连接ED、EC,则△CDE周长的最小值为( )| A. | 3$\sqrt{5}$ | B. | 3$\sqrt{3}$ | C. | 3$\sqrt{3}$+3 | D. | 3$\sqrt{5}$+3 |
19.某车间有技工85人,平均每人每天可加工甲种部件16个或乙种部件10个,2个甲种部件和3个乙种部件正好配成一套.要使每天加工的甲、乙两种部件刚好配套,则应安排加工甲、乙两种部件的人数分别为多少人?
20.某项工作甲单独做需要4天完成,乙单独做需要6天完成,若乙先做1天,然后再由甲、乙合作完成此项工作,若设甲乙合作需x天完成,则可列的方程为( )
| A. | 1+($\frac{1}{4}$+$\frac{1}{6}$)x=1 | B. | $\frac{1}{4}$+($\frac{1}{4}$+$\frac{1}{6}$)x=1 | C. | $\frac{1}{6}$+($\frac{1}{4}$+$\frac{1}{6}$)x=1 | D. | $\frac{1}{6}$+$\frac{(4+6)}{2}$x=1 |
 探究题:
探究题: