题目内容
8.甲、乙两车间同生产一种零件,甲车间有1人每天生产6件,其余每人每天生产11件,乙车间有1人每天生产7件,其余的生产10件,已知各车间生产的零件总数相等,且不少于100件不超过200件,求甲、乙车间各多少人?分析 根据各车间生产的零件总数相等和不少于100件不超过200件列出不等式组解决问题即可.
解答 解:设甲车间的人数为x人,乙车间的人数为y人,可得:6+11(x-1)=7+10(y-1),
可得:y=$\frac{11x-2}{10}$,
根据题意可得不等式组:$\left\{\begin{array}{l}{6+11(x-1)≥100}\\{6+11(x-1)≤200}\end{array}\right.$,
解得:$9\frac{6}{11}≤x≤18\frac{7}{11}$,
因为x,y取整数,
所以:x=12,y=13,
答:甲、乙车间各12,13人.
点评 此题主要考查了不等式的应用,根据已知得出正确的不等式关系是解题关键.

练习册系列答案
相关题目
19.某车间有技工85人,平均每人每天可加工甲种部件16个或乙种部件10个,2个甲种部件和3个乙种部件正好配成一套.要使每天加工的甲、乙两种部件刚好配套,则应安排加工甲、乙两种部件的人数分别为多少人?
20.某项工作甲单独做需要4天完成,乙单独做需要6天完成,若乙先做1天,然后再由甲、乙合作完成此项工作,若设甲乙合作需x天完成,则可列的方程为( )
| A. | 1+($\frac{1}{4}$+$\frac{1}{6}$)x=1 | B. | $\frac{1}{4}$+($\frac{1}{4}$+$\frac{1}{6}$)x=1 | C. | $\frac{1}{6}$+($\frac{1}{4}$+$\frac{1}{6}$)x=1 | D. | $\frac{1}{6}$+$\frac{(4+6)}{2}$x=1 |
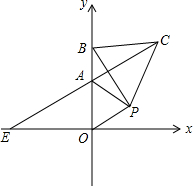 如图,在平面直角坐标系中,△AOP为等边三角形,A(0,a),P(b,c),且(a-2)2+|b-$\sqrt{3}$|+c2-2c+1=0,点B为y轴上一动点,以BP为边作等边三角形△PBC.
如图,在平面直角坐标系中,△AOP为等边三角形,A(0,a),P(b,c),且(a-2)2+|b-$\sqrt{3}$|+c2-2c+1=0,点B为y轴上一动点,以BP为边作等边三角形△PBC.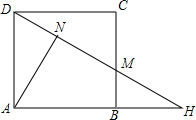 如图,四边形ABCD是边长为4的正方形,点H是AB延长线上一点,连结DH,交BC于M,分别过A点作AN⊥DH,垂足为点N.
如图,四边形ABCD是边长为4的正方形,点H是AB延长线上一点,连结DH,交BC于M,分别过A点作AN⊥DH,垂足为点N. 如图是一个正方体的展开图,标注了字母a的面是正方体的正面.如果正方体相对两个面上的式子的值相等,求(y-x)2015的值.
如图是一个正方体的展开图,标注了字母a的面是正方体的正面.如果正方体相对两个面上的式子的值相等,求(y-x)2015的值.