题目内容
12．
如图，在正方形ABCD中，E是CD上一点，F是CB延长线上一点，且DE=BF，AF，AE之间有怎样的关系？请说明理由．
分析 根据正方形的性质得到∠D=∠ABC=∠BAD=90°，推出∠D=∠ABF=90°，证得△ADE≌△ABF，根据全等三角形的性质得到AE=AF，∠EAD=∠FAB，然后根据余角的性质即可得到结论．
解答 解：AF=AE，AF⊥AE，
在正方形ABCD中，
∵∠D=∠ABC=∠BAD=90°，
∴∠ABF=90°，
∴∠D=∠ABF=90°，
在△ADE与△ABF中，
$\left\{\begin{array}{l}{AD=AB}\\{∠D=∠ABF}\\{DE=BF}\end{array}\right.$，
∴△ADE≌△ABF，
∴AE=AF，∠EAD=∠FAB，
∵∠BAD=90°，
∴∠DAE+∠EAB=90°
∴∠FAB+∠EAB=90°，
∴AF⊥AE．
点评 本题考查了全等三角形的判定和性质，正方形的性质，余角的性质，熟练掌握全等三角形的判定定理是解题的关键．
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
2．
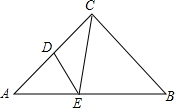如图，在Rt△ABC中，∠ACB=90°，AC=BC=6，D为AC的中点，E是线段AB边上一动点，连接ED、EC，则△CDE周长的最小值为（ ）
如图，在Rt△ABC中，∠ACB=90°，AC=BC=6，D为AC的中点，E是线段AB边上一动点，连接ED、EC，则△CDE周长的最小值为（ ）| A． | 3$\sqrt{5}$ | B． | 3$\sqrt{3}$ | C． | 3$\sqrt{3}$+3 | D． | 3$\sqrt{5}$+3 |
20．某项工作甲单独做需要4天完成，乙单独做需要6天完成，若乙先做1天，然后再由甲、乙合作完成此项工作，若设甲乙合作需x天完成，则可列的方程为（ ）
| A． | 1+（$\frac{1}{4}$+$\frac{1}{6}$）x=1 | B． | $\frac{1}{4}$+（$\frac{1}{4}$+$\frac{1}{6}$）x=1 | C． | $\frac{1}{6}$+（$\frac{1}{4}$+$\frac{1}{6}$）x=1 | D． | $\frac{1}{6}$+$\frac{（4+6）}{2}$x=1 |
如图，在平面直角坐标系中，点A的坐标是（1，2），连接OA，将线段OA绕着点O顺时针旋转，使点A的对应点A′恰好落在x轴正半轴上，则点A′的坐标是（$\sqrt{5}$，0）．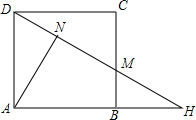
如图，四边形ABCD是边长为4的正方形，点H是AB延长线上一点，连结DH，交BC于M，分别过A点作AN⊥DH，垂足为点N．