题目内容
已知点A、B、C在平面直角坐标系中，A（0，4），B（3，3），C（3，1）．连接A、B、C成一个三角形，将此三角形绕点C按顺时针方向旋转90°得到△A′B′C′．求：
（1）线段CA所扫过的面积；
（2）线段AB扫过的面积；
（3）△ABC扫过的面积．
（1）线段CA所扫过的面积；
（2）线段AB扫过的面积；
（3）△ABC扫过的面积．
考点：作图-旋转变换,扇形面积的计算
专题：计算题
分析：（1）线段CA扫过的面积为扇形ACA′的面积，求出即可；
（2）线段AB扫过的面积为扇形ACA′面积减去扇形BCB′面积，求出即可；
（3）三角形ABC扫过的面积为扇形ACA′面积加上扇形BCB′面积，求出即可．
（2）线段AB扫过的面积为扇形ACA′面积减去扇形BCB′面积，求出即可；
（3）三角形ABC扫过的面积为扇形ACA′面积加上扇形BCB′面积，求出即可．
解答：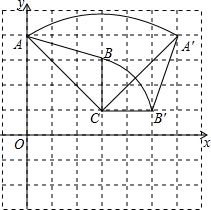
解：（1）如图所示，线段CA扫过的面积S=
=
；
（2）如图所示，线段AB扫过的面积S=S扇形ACA′-S扇形BCB′=
-
=
；
（3）如图所示，△ABC扫过的面积S=S扇形ACA′+S扇形BCB′=
+
=
．
解：（1）如图所示，线段CA扫过的面积S=90π×(3
| ||
| 360 |
| 27π |
| 4 |
（2）如图所示，线段AB扫过的面积S=S扇形ACA′-S扇形BCB′=
| 27π |
| 4 |
| 90π×22 |
| 360 |
| 23π |
| 4 |
（3）如图所示，△ABC扫过的面积S=S扇形ACA′+S扇形BCB′=
| 27π |
| 4 |
| 90π×22 |
| 360 |
| 31π |
| 4 |
点评：此题考查了作图-旋转变换，以及扇形面积的计算，熟练掌握扇形面积公式是解本题的关键．
练习册系列答案
相关题目
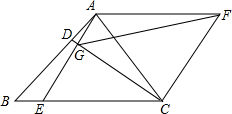如图，△ABC和△ACF均为等边三角形，点D、E分别为AD，BE边上的点，且AD=BE，AE与CD交于G点，连接GF．
如图，已知△ABC为等边三角形，O为其内部一点，将△AOC绕点A旋转60°得到△ADB，连接OD，DB，已知AO=3cm，BO=5cm，CO=4cm，求△ODB的周长．
已知Rt△ACB中，∠ACB=90°，CA=CB，过C任作CD，AD⊥CD于D，BE⊥CD于E，问：AD、ED、BE之间有什么数量关系？证明你的结论．
如图所示，用两个钢索加固直立的电线杆，若要使AB与AC的长相等，需添加条件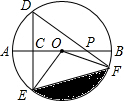
如图，AB是⊙O的直径，弦DE垂直平分半径OA，C为垂足，弦DF与半径OB相交于点P，连接EF、EO，若DE=4