题目内容
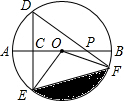 如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连接EF、EO,若DE=4
如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连接EF、EO,若DE=4| 3 |
(1)求⊙O的半径;
(2)求图中阴影部分的面积.
考点:垂径定理,勾股定理,扇形面积的计算
专题:计算题
分析:(1)根据垂径定理得CE=
DE=2
,而弦DE平分半径OA,所以OC=
OE,根据含30度的直角三角形三边的关系得到∠CEO=30°,则OC=
CE=2,所以OE=4;
(2)先利用圆周角定理得到∠EOF=2∠D=90°,然后扇形的面积公式和图中阴影部分的面积=S扇形EOF-S△EOF进行计算即可.
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 3 |
(2)先利用圆周角定理得到∠EOF=2∠D=90°,然后扇形的面积公式和图中阴影部分的面积=S扇形EOF-S△EOF进行计算即可.
解答:解:(1)∵OA⊥DE,
∴CD=CE=
DE=2
,
∵弦DE平分半径OA,
∴OC=
OE,
∴∠CEO=30°,
∴OC=
CE=
•2
=2,
∴OE=2OC=4,
即⊙O的半径为4;
(2)∵∠EOF=2∠D=2×45°=90°,
∴图中阴影部分的面积=S扇形EOF-S△EOF
=
-
•42
=4π-8.
∴CD=CE=
| 1 |
| 2 |
| 3 |
∵弦DE平分半径OA,
∴OC=
| 1 |
| 2 |
∴∠CEO=30°,
∴OC=
| ||
| 3 |
| ||
| 3 |
| 3 |
∴OE=2OC=4,
即⊙O的半径为4;
(2)∵∠EOF=2∠D=2×45°=90°,
∴图中阴影部分的面积=S扇形EOF-S△EOF
=
| 90•π•42 |
| 360 |
| 1 |
| 2 |
=4π-8.
点评:本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了扇形的面积公式.

练习册系列答案
相关题目
 在一个大圆盘中有4个小圆盘,已知大小圆盘的直径都是整数,阴影部分的面积为7πcm2.求大小圆盘的半径是多少?
在一个大圆盘中有4个小圆盘,已知大小圆盘的直径都是整数,阴影部分的面积为7πcm2.求大小圆盘的半径是多少? 数a、b在数轴上的位置如图,则-a
数a、b在数轴上的位置如图,则-a