题目内容
1.某商场销售一种成本为每件30元的商品,销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似看作一次函数y=-10x+600,商场销售该商品每月获得利润为w(元).(1)求w与x之间的函数关系式;
(2)如果商场销售该商品每月想要获得2000元的利润,那么每月成本至少多少元?
(3)为了保护环境,政府部门要求用更加环保的新产品替代该商品,商场销售新产品,每月的销量与销售价格之间的关系与原产品的销售情况相同,新产品的成本每件32元,若新产品每月的销售量不低于200件时,政府部门给予每件4元的补贴,试求定价多少时,每月销售新产品的利润最大?求出最大的利润.
分析 (1)根据:月利润=(销售单价-成本价)×销售量,从而列出关系式;
(2)令w=2000,然后解一元二次方程,从而求出销售单价,再根据:月成本=成本价×销售量可得答案;
(3)根据销售量低于200件和不低于200件求出x的范围,并根据:利润=每件产品的利润×销售量,从而列出关系式;运二次函数性质求出其最值,比较大小可得.
解答 解:(1)w=(x-30)(-10x+600)=-10x2+900x-18000.
(2)由题意得,-10x2+900x-18000=2000,
解得:x1=40,x2=50,
当x=40时,成本为30×(-10×40+600)=6000(元),
当x=50时,成本为30×(-10×50+600)=3000(元),
∴每月想要获得2000元的利润,每月成本至少3000元.
(3)当y<200时,即:-10x+600<200,解得:x>40,
w=(x-32)(-10x+600)=-10(x-46)2+1960,
∵a=-10<0,x>40,
∴当x=46时,w最大值=1960(元);
当y≥200时,即:-10x+600≥200,解得:x≤40,
w=(x-32+4)(-10x+600)=-10(x-44)2+2560,
∵a=-10<0,
∴抛物线开口向下,当32<x≤40时,w随x的增大而增大,
∴当x=40时,w最大值=2400(元),
∵1960<2400,
∴当x=40时,w最大,
答:定价每件40元时,每月销售新产品的利润最大,最大利润为2400元.
点评 本题考查了把实际问题转化为二次函数,再利用二次函数的性质进行实际应用.根据题意分情况建立二次函数的模型是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.不等式组$\left\{\begin{array}{l}{3x<2x+4}\\{x-1≥2}\end{array}\right.$的解集是( )
| A. | x>4 | B. | x≤3 | C. | 3≤x<4 | D. | 无解 |
13. 在数轴上标注了四段范围,如图所示,则表示-$\sqrt{10}$的点落在( )
在数轴上标注了四段范围,如图所示,则表示-$\sqrt{10}$的点落在( )
 在数轴上标注了四段范围,如图所示,则表示-$\sqrt{10}$的点落在( )
在数轴上标注了四段范围,如图所示,则表示-$\sqrt{10}$的点落在( )| A. | 段① | B. | 段② | C. | 段③ | D. | 段④ |
11.月亮超市正在热销某种商品,其标价为每件10元,若这种商品打7折销售,则每件可获利1元,设该商品每件的进价为x元,根据题意可列出的一元一次方程为( )
| A. | 10×0.7-x=1 | B. | 10-x×0.7=1 | C. | (10-x)×0.7=1 | D. | 10-x=1×0.7 |
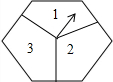 如图是一个能自由转动的正六边形转盘,这个转盘被三条分割线分成形状相同,面积相等的三部分,且分别标有“1”、“2”、“3”三个数字,指针的位置固定不动,让转盘自由转动两次,当每次转盘停止后,记录指针指向的数(当指针指向分割线时,视其指向分割线左边的区域),则两次指针指向的数都是奇数的概率为$\frac{4}{9}$.
如图是一个能自由转动的正六边形转盘,这个转盘被三条分割线分成形状相同,面积相等的三部分,且分别标有“1”、“2”、“3”三个数字,指针的位置固定不动,让转盘自由转动两次,当每次转盘停止后,记录指针指向的数(当指针指向分割线时,视其指向分割线左边的区域),则两次指针指向的数都是奇数的概率为$\frac{4}{9}$.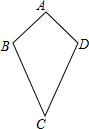 有这样一个问题:如图,在四边形ABCD中,AB=AD,CB=CD,我们把这种两组邻边分别相等的四边形叫做筝形,请探究筝形的性质和判定方法.
有这样一个问题:如图,在四边形ABCD中,AB=AD,CB=CD,我们把这种两组邻边分别相等的四边形叫做筝形,请探究筝形的性质和判定方法.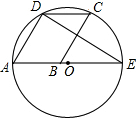 如图,已知平行四边形ABCD的顶点A、D、C在⊙O上,顶点B在⊙O的直径AE上,连接DE,若∠E=32°,则∠C=58°.
如图,已知平行四边形ABCD的顶点A、D、C在⊙O上,顶点B在⊙O的直径AE上,连接DE,若∠E=32°,则∠C=58°.