Question

9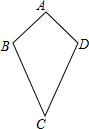．有这样一个问题：如图，在四边形ABCD中，AB=AD，CB=CD，我们把这种两组邻边分别相等的四边形叫做筝形，请探究筝形的性质和判定方法．
小南根据学习四边形的经验，对筝形的性质和判定方法进行了探究．
下面是小南的探究过程：
（1）由筝形的定义可知，筝形的边的性质时：筝形的两组邻边分别相等，关于筝形的角的性质，通过测量，折纸的方法，猜想：筝形有一组对角相等．
请将下面证明此猜想的过程补充完整：
已知：如图，在筝形ABCD中，AB=AD，CB=CD．
求证：∠B=∠C．
由以上证明可得，筝形的角的性质是：筝形有一组对角相等．
（2）连接筝形的两条对角线，探究发现筝形的另一条性质：筝形的一条对角线平分另一条对角线，结合图形，写出筝形的其他性质（一条即可）：筝形的两条对角线互相垂直
（3）筝形的定义是判定一个四边形为筝形的方法之一，试判断命题“一组对角相等，一条对角线平分另一条对角线的四边形是”是否成立？如果成立，请给出证明；如果不成立，请举出一个反例，画出图形，并加以证明．

Answer 1

分析 （1）证明：连接AC，根据全等三角形的性质得到∠B=∠C．
（2）根据轴对称图形的性质得到结论；
（3）不成立，举反例说明即可．

解答 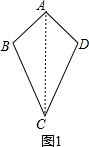（1）证明：如图1，连接AC，
在△ABC和△ADC中，
$\left\{\begin{array}{l}{AB=AD}\\{CB=CD}\\{AC=AC}\end{array}\right.$，
∴△ABC≌△ADC，
∴∠B=∠C，
故答案为：∠B=∠C；

（2）解：筝形的两条对角线互相垂直，筝形的一条对角线平分一组对角，筝形是轴对称图形；

（3）解：不成立，
证明反例如图2所示，
在平行四边形ABCD中，AB≠AD，对角线相交于点O，
由平行四边形的性质可知
此图形满足∠ABC=∠ADC，AC平分BD，但是四边形ABCD不是筝形．

点评 本题考查了轴对称图形，图形的对称以及全等三角形的判定，正确证明△BAC≌△DAC是解决本题的关键．