题目内容
6.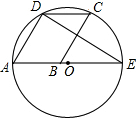 如图,已知平行四边形ABCD的顶点A、D、C在⊙O上,顶点B在⊙O的直径AE上,连接DE,若∠E=32°,则∠C=58°.
如图,已知平行四边形ABCD的顶点A、D、C在⊙O上,顶点B在⊙O的直径AE上,连接DE,若∠E=32°,则∠C=58°.
分析 由AE是⊙O的直径,根据直径所对的圆周角是直角,可求得∠ADE=90°,继而求得∠A的度数,然后由平行四边形的性质,求得答案.
解答 解:∵AE是⊙O的直径,
∴∠ADE=90°,
∵∠E=32°,
∴∠A=90°-∠E=58°,
∵四边形ABCD是平行四边形,
∴∠C=∠A=58°,
故答案为:58°.
点评 此题考查了圆周角定理以及平行四边形的性质.注意半圆(或直径)所对的圆周角是直角是解答此题的关键.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
8.不等式组$\left\{\begin{array}{l}{x-1>1}\\{x+8<4x-1}\end{array}\right.$的解集是( )
| A. | x>3 | B. | x<3 | C. | x<2 | D. | x>2 |
9.近几年来,我市加大教育信息化投入,投资201000000元,初步完成咸宁市教育公共云服务平台基础工程,教学点数字教育资源全覆盖,将201000000用科学记数法表示为( )
| A. | 20.1×107 | B. | 2.01×108 | C. | 2.01×109 | D. | 0.201×1010 |
15.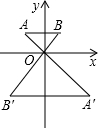 如图,已知△OAB与△OA′B′是相似比为 1:2 的位似图形,点O为位似中心,若△OAB内一点P(x,y)与△OA′B′内一点P′是一对对应点,则点P′的坐标为( )
如图,已知△OAB与△OA′B′是相似比为 1:2 的位似图形,点O为位似中心,若△OAB内一点P(x,y)与△OA′B′内一点P′是一对对应点,则点P′的坐标为( )
 如图,已知△OAB与△OA′B′是相似比为 1:2 的位似图形,点O为位似中心,若△OAB内一点P(x,y)与△OA′B′内一点P′是一对对应点,则点P′的坐标为( )
如图,已知△OAB与△OA′B′是相似比为 1:2 的位似图形,点O为位似中心,若△OAB内一点P(x,y)与△OA′B′内一点P′是一对对应点,则点P′的坐标为( )| A. | (-x,-y) | B. | (-2x,-2y) | C. | (-2x,2y) | D. | (2x,-2y) |
 如图,在平面直角坐标系中,已知抛物线y=ax2+bx的对称轴为x=$\frac{3}{4}$,且经过点A(2,1),点P是抛物线上的动点,其横坐标为m(0<m<2),过点P作PB⊥x轴,垂足为B,交OA于点C.点O关于直线PB的对称点为D,连接CD、AD,过点A作AE⊥x轴,垂足为E.
如图,在平面直角坐标系中,已知抛物线y=ax2+bx的对称轴为x=$\frac{3}{4}$,且经过点A(2,1),点P是抛物线上的动点,其横坐标为m(0<m<2),过点P作PB⊥x轴,垂足为B,交OA于点C.点O关于直线PB的对称点为D,连接CD、AD,过点A作AE⊥x轴,垂足为E.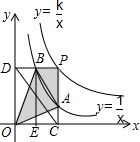 两个反比例函数y=$\frac{k}{x}$(k>1)和y=$\frac{1}{x}$在第一象限内的图象如图所示,点P在y=$\frac{k}{x}$的图象上,PC⊥x轴于点C,交y=$\frac{1}{x}$的图象于点A,PD⊥y轴于点D,交y=$\frac{1}{x}$的图象于点B,BE⊥x轴于点E,当点P在y=$\frac{k}{x}$的图象上运动时,以下结论:
两个反比例函数y=$\frac{k}{x}$(k>1)和y=$\frac{1}{x}$在第一象限内的图象如图所示,点P在y=$\frac{k}{x}$的图象上,PC⊥x轴于点C,交y=$\frac{1}{x}$的图象于点A,PD⊥y轴于点D,交y=$\frac{1}{x}$的图象于点B,BE⊥x轴于点E,当点P在y=$\frac{k}{x}$的图象上运动时,以下结论: 平面直角坐标系中有直线y=kx-k+4(k≠0),
平面直角坐标系中有直线y=kx-k+4(k≠0),