题目内容
15.在△ABC中,AB=AC,BD平分∠ABC,交AC于D点,若BD=BC,求∠DBC的度数.分析 设∠C=2x,利用等腰三角形的性质得到∠ABC=∠C=2x,∠BDC=∠C=2x,再根据角平分线的定义得∠ABD=∠CBD=$\frac{1}{2}$∠ABC=x,根据三角形内角和为180°求出x的值即可.
解答 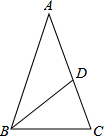 解:设∠C=2x,
解:设∠C=2x,
∵AB=AC,
∴∠ABC=∠C=2x,
∵BD=BC,
∴∠BDC=∠C=2x,
∵BD平分∠ABC,
∴∠ABD=∠CBD=$\frac{1}{2}$∠ABC=x,
∵∠BDC=∠A+∠ABD,
∴∠A=2x-x=x,
∴x+2x+2x=180°,
∴x=36°,
∴∠DBC=36°.
点评 本题主要考查了等腰三角形的性质,解题的关键是用x表示出∠A的度数,此题难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.等腰三角形的一个外角为60°,则它的顶角的度数为( )
| A. | 120° | B. | 90° | C. | 60° | D. | 30° |
3. 如图,不能判定AB∥CD的是( )
如图,不能判定AB∥CD的是( )
 如图,不能判定AB∥CD的是( )
如图,不能判定AB∥CD的是( )| A. | ∠2=∠3 | B. | ∠1=∠4 | C. | ∠1=∠2 | D. | ∠1=∠3 |
 如图,B村位于一条河的一岸,现在要将河里的水通过修建水渠引到村里进行使用,问:这条水渠该如何修,才能使到A村的距离最短,请画出图形,并说明理由?(画图可借助三角板,量角器等工具)
如图,B村位于一条河的一岸,现在要将河里的水通过修建水渠引到村里进行使用,问:这条水渠该如何修,才能使到A村的距离最短,请画出图形,并说明理由?(画图可借助三角板,量角器等工具)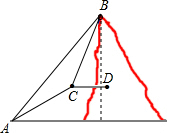 如图,小明和小强攀登一无名山峰,他俩在山脚A处测得主峰B的仰角为45°,然后从山脚沿一段倾角为30°的斜坡走了2km到达山腰C,此时测得主峰B的仰角为60°,于是小明对小强说:“我知道主峰多高了.”你能根据他们的数据算出主峰的高度吗?
如图,小明和小强攀登一无名山峰,他俩在山脚A处测得主峰B的仰角为45°,然后从山脚沿一段倾角为30°的斜坡走了2km到达山腰C,此时测得主峰B的仰角为60°,于是小明对小强说:“我知道主峰多高了.”你能根据他们的数据算出主峰的高度吗?