题目内容
如图,已知A、B两点的坐标分别为A(2
,0),B(0,2),点P是△AOB外接圆上的一点,且∠AOP=45°
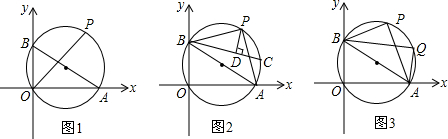
(1)如图1,求点P的坐标;
(2)如图2,连接BP、AP,C为弧PA上一点,过P作PD⊥BC于D点,求证:BD=CD+AC;
(3)如图3,点Q是弧AP上一动点(不与A、P重合),连接PQ、AQ、BQ,求:
的值.
| 3 |
(1)如图1,求点P的坐标;
(2)如图2,连接BP、AP,C为弧PA上一点,过P作PD⊥BC于D点,求证:BD=CD+AC;
(3)如图3,点Q是弧AP上一动点(不与A、P重合),连接PQ、AQ、BQ,求:
| BQ-AQ |
| PQ |

考点:圆的综合题
专题:综合题
分析:(1)作PH⊥x轴于H,连结PA、PB,根据圆周角定理由∠AOB=90°,得到AB为△AOB外接圆的直径,则∠BPA=90°,再利用勾股定理计算出AB=4,由根据圆周角定理由∠AOP=45°得到∠PBA=45°,则可判断△PAB和△POH都为等腰直角三角形,所以PA=
AB=2
,PH=OH,设OH=t,则PH=t,AH=2
-t,在Rt△PHA中,根据勾股定理得到t2+(2
-t)2=(2
)2,解得t1=
+1,t2=
-1(舍去),于是得到P点坐标为(
+1,
+1);
(2)作PE⊥AC,交AC的延长线于E,根据圆周角定理由AB为直径得到∠ACB=90°,易得四边形PDCE为矩形,由于PA=PB,∠PBC=∠PAE,则可判断△PBD≌△PAE,则PD=PE,BD=AE,所以四边形PDCE为正方形,得到CD=CE,所以BD=AE=CE+AC=CD+AC;
(3)作PD⊥BQ于D,利用(2)中的结论得BD=DQ+AQ,则BQ-AQ=2DQ,所以
=
,根据圆周角定理得∠PQB=∠PAB=45°,则可判断△PDQ为等腰直角三角形,则PQ=
DQ,所以
=
=
.
| ||
| 2 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
(2)作PE⊥AC,交AC的延长线于E,根据圆周角定理由AB为直径得到∠ACB=90°,易得四边形PDCE为矩形,由于PA=PB,∠PBC=∠PAE,则可判断△PBD≌△PAE,则PD=PE,BD=AE,所以四边形PDCE为正方形,得到CD=CE,所以BD=AE=CE+AC=CD+AC;
(3)作PD⊥BQ于D,利用(2)中的结论得BD=DQ+AQ,则BQ-AQ=2DQ,所以
| BQ-AQ |
| PQ |
| 2DQ |
| PQ |
| 2 |
| BQ-AQ |
| PQ |
| 2DQ |
| PQ |
| 2 |
解答:(1)解:作PH⊥x轴于H,连结PA、PB,如图1,
∵∠AOB=90°,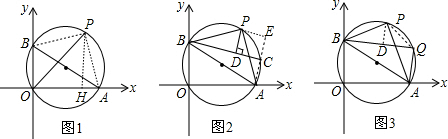
∴AB为△AOB外接圆的直径,
∴∠BPA=90°,
∵A(2
,0),B(0,2),
∴OA=2
,OB=2,
∴AB=
=4,
∵∠AOP=45°,
∴∠PBA=45°,
∴△PAB和△POH都为等腰直角三角形,
∴PA=
AB=2
,PH=OH,
设OH=t,则PH=t,AH=2
-t,
在Rt△PHA中,
∵PH2+AH2=PA2,
∴t2+(2
-t)2=(2
)2,
整理得t2-2
t+2=0,解得t1=
+1,t2=
-1(舍去),
∴P点坐标为(
+1,
+1);
(2)证明:作PE⊥AC,交AC的延长线于E,如图2,
∵AB为直径,
∴∠ACB=90°,
∵PD⊥BC,
∴四边形PDCE为矩形,
在△PBD和△PAE中,
,
∴△PBD≌△PAE(AAS),
∴PD=PE,BD=AE,
∴四边形PDCE为正方形,
∴CD=CE,
∴BD=AE=CE+AC=CD+AC;
(3)解:作PD⊥BQ于D,如图3,
由(2)得BD=DQ+AQ,
∴BQ-AQ=BD+DQ-AQ=DQ+AQ+DQ-AQ=2DQ,
∴
=
,
∵∠PQB=∠PAB=45°,
∴△PDQ为等腰直角三角形,
∴PQ=
DQ,
∴
=
=
=
.
∵∠AOB=90°,

∴AB为△AOB外接圆的直径,
∴∠BPA=90°,
∵A(2
| 3 |
∴OA=2
| 3 |
∴AB=
| OA2+OB2 |
∵∠AOP=45°,
∴∠PBA=45°,
∴△PAB和△POH都为等腰直角三角形,
∴PA=
| ||
| 2 |
| 2 |
设OH=t,则PH=t,AH=2
| 3 |
在Rt△PHA中,
∵PH2+AH2=PA2,
∴t2+(2
| 3 |
| 2 |
整理得t2-2
| 3 |
| 3 |
| 3 |
∴P点坐标为(
| 3 |
| 3 |
(2)证明:作PE⊥AC,交AC的延长线于E,如图2,
∵AB为直径,
∴∠ACB=90°,
∵PD⊥BC,
∴四边形PDCE为矩形,
在△PBD和△PAE中,
|
∴△PBD≌△PAE(AAS),
∴PD=PE,BD=AE,
∴四边形PDCE为正方形,
∴CD=CE,
∴BD=AE=CE+AC=CD+AC;
(3)解:作PD⊥BQ于D,如图3,
由(2)得BD=DQ+AQ,
∴BQ-AQ=BD+DQ-AQ=DQ+AQ+DQ-AQ=2DQ,
∴
| BQ-AQ |
| PQ |
| 2DQ |
| PQ |
∵∠PQB=∠PAB=45°,
∴△PDQ为等腰直角三角形,
∴PQ=
| 2 |
∴
| BQ-AQ |
| PQ |
| 2DQ |
| PQ |
| 2DQ | ||
|
| 2 |
点评:本题考查了圆的综合题:熟练掌握圆周角定理、全等三角形的判定与性质和等腰直角三角形的性质;会利用勾股定理计算线段的长.

练习册系列答案
相关题目
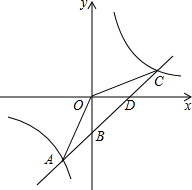 如图,一次函数y=kx+b的图象与反比例函数y=
如图,一次函数y=kx+b的图象与反比例函数y= 如图,在△ABC中,∠ABC=2∠C,AD平分∠BAC,求证:AB+BD=AC.
如图,在△ABC中,∠ABC=2∠C,AD平分∠BAC,求证:AB+BD=AC.