题目内容
一个事件发生的概率不可能是( )
A. 0 B. 1 C.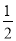 
D. 
D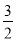
【解析】因为一个事件发生的概率不可能大于1,故选D.
中考解读考点精练系列答案
各地期末复习特训卷系列答案已知(b＋2)xb＋1＜－3是关于x的一元一次不等式，试求b的值，并解这个一元一次不等式．
x＜－1.5.
【解析】试题分析：先根据一元一次不等式的概念，知b+1=0，求得b，然后代入解不等式即可.
试题解析：∵(b＋2)xb＋1＜－3是关于x的一元一次不等式，
∴b＋1＝1，则b＝0，
∴2x＜－3，
解得x＜－1.5. 一个直角三角形的两条直角边长分别为6 cm和8 cm，那么这个直角三角形的斜边长为（ ）
A. 6 cm B. 8 cm C. 10 cm D. 24 cm
C
【解析】根据勾股定理可以得出：斜边长==10cm.
故选：C． 计算：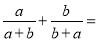 
________．
1
【解析】试题分析：原式＝
＝
＝1．
故答案为：1． 某小组做“用频率估计概率”的试验时,统计了某一结果出现的频率,绘制了如图所示的折线统计图,则符合这一结果的试验最有可能的是( )
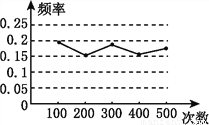
A. 在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B. 一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
C. 暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一个球是黄球
D. 掷一个质地均匀的正方体骰子,向上的面的点数是4
D
【解析】试题解析：A、在“石头、剪刀、布”的游戏中，小明随机出的是“剪刀“的概率为，故A选项错误；
B、一副去掉大小王的普通扑克牌洗匀后，从中任抽一张牌的花色是红桃的概率是： ；故B选项错误；
C、暗箱中有1个红球和2个黄球，它们只有颜色上的区别，从中任取一球是黄球的概率为，故C选项错误；
D、掷一个质地均匀的正六面体骰子，向上的面点数是4的概率为≈0.17，故D选项正... 如图，点E是正方形ABCD内的一点，连接AE、BE、CE，将△ABE绕点B顺时针旋转90°到△CBE′的位置．若AE=1，BE=2，CE=3，则∠BE′C=__度．
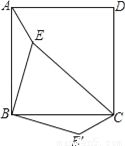
135
【解析】试题分析：首先根据旋转的性质得出，△EBE′是直角三角形，进而得出∠BEE′=∠BE′E=45°，即可得出答案．
【解析】
连接EE′
∵△ABE绕点B顺时针旋转90°到△CBE′
∴∠EBE′是直角，∴△EBE′是直角三角形，
∵△ABE与△CE′B全等
∴BE=BE′=2，∠AEB=∠BE′C
∴∠BEE′=∠BE′E=45°，
... 已知下列命题：
①若a≤0，则|a|=﹣a；
②若ma2＞na2，则m＞n；
③两组对角分别相等的四边形是平行四边形；
④垂直于弦的直径平分弦．
其中原命题与逆命题均为真命题的个数是（ ）
A. 1个 B. 2个 C. 3个 D. 4个
B
【解析】①若a≤0，则|a|=﹣a是真命题，逆命题为若|a|=﹣a，则a≤0是真命题，
②若ma2＞na2，则m＞n是真命题，逆命题为若m＞n，则ma2＞na2是假命题，
③两组对角分别相等的四边形是平行四边形是真命题，逆命题为平行四边形的两组对角分别相等是真命题，
④垂直于弦的直径平分弦是真命题，逆命题为平分弦的直径垂直于弦是假命题，
所以原命题与逆命题均为真命... 如图是若干张卡片，它们的背面都一样，现将它们背面朝上，从中任意摸一张卡片，摸到几号卡片的频率大？
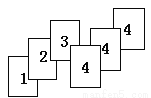
摸到4号卡片的频率大.
【解析】试题分析: 本题考察可能性大小的应用，根据不同编号卡片的数量求出不同编号卡片被抽到的概率是解答本题的关键.
解答：因为给出的六张卡片中，1号卡片有1张，2号有1张，3号有1张，4号有3张.所以摸到1号卡片的频率为，摸到2号卡片的频率为，摸到3号卡片的频率为，摸到4号卡片的频率为.所以，摸到4号卡片的频率大. 如图，有A、B、C三个居民小区的位置成三角形，现决定在三个小区之间修建一个购物超市，使超市到三个小区的距离相等，则超市应建在( )
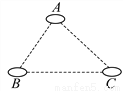
A. 在AC、BC两边高线的交点处 B. 在AC、BC两边中线的交点处
C. 在∠A、∠B两内角平分线的交点处 D. 在AC、BC两边垂直平分线的交点处
D
【解析】根据线段的垂直平分线的性质：线段的垂直平分线上的点到线段的两个端点的距离相等可得：
超市应建在△ABC三条边的垂直平分线的交点处．
故选D．