题目内容
已知(b＋2)xb＋1＜－3是关于x的一元一次不等式，试求b的值，并解这个一元一次不等式．
x＜－1.5.
【解析】试题分析：先根据一元一次不等式的概念，知b+1=0，求得b，然后代入解不等式即可.
试题解析：∵(b＋2)xb＋1＜－3是关于x的一元一次不等式，
∴b＋1＝1，则b＝0，
∴2x＜－3，
解得x＜－1.5.
练习册系列答案
相关题目
已知抛物线和直线l在同一直角坐标系中的图象如图所示，抛物线的对称轴为直线x=﹣1，P1（x1，y1），P2（x2，y2）是抛物线上的点，P3（x3，y3）是直线l上的点，且x3＜﹣1＜x1＜x2，则y1，y2，y3的大小关系是（ ）
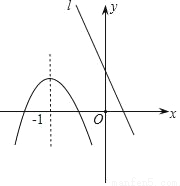
A. y1＜y2＜y3 B. y2＜y3＜y1 C. y3＜y1＜y2 D. y2＜y1＜y3
D
【解析】因为抛物线的对称轴为直线x=-1，开口向下，P1（x1，y1），P2（x2，y2）是抛物线上的点，且-1＜x1＜x2，根据二次函数的性质：在对称轴的右侧，y随x的增大而减小，可得y2＜ y1；P3（x3，y3）是直线l上的点，直线y随x的增大而减小，且x3＜-1，由图象可知，直线上x3对应的函数值y3大于-1对应的函数值，又因x=-1时，抛物线的顶点最高，可得y3最大，所以y2＜... 在□ABCD中，∠A∶∠B∶∠C∶∠D的值可以是（ ）
A.1∶2∶3∶4 B.1∶2∶2∶1
C.1∶1∶2∶2 D.2∶1∶2∶1
D．
【解析】
试题解析：∵四边形ABCD是平行四边形，
∴∠A=∠C，∠B=∠D，AB∥CD，
∴∠B+∠C=180°，∠A+∠D=180°，
即∠A和∠C的数相等，∠B和∠D的数相等，且∠B+∠C=∠A+∠D，
故选D． A、B、C、D在同一平面内，从①AB∥CD；②AB＝CD；③BC∥AD；④BC＝AD；这四个条件中任选两个，能使四边形ABCD成为平行四边形的选法共有（ ）
A. 3种 B 4种 C 5种 D 6种
B
【解析】试题分析：根据一组对边平行且相等、两组对边分别平行、两组对边分别相等来进行判定.则正确的选法为：①③、②④、①②、③④四种判定方法. 辽宁南部素以“苹果之乡”著称，某乡组织10辆汽车装运A、B两种苹果到外地销售，按规定每辆汽车只装同一种苹果，且必须装满．已知A、B两种苹果的每辆车运载量及每吨苹果获利如下表：
苹果品种 | A | B |
每辆汽车运载量(吨) | 3 | 2 |
每吨苹果获利(百元) | 5 | 9 |
(1)要求共运出苹果至少24吨，试写出装运A种苹果的汽车x(辆)应满足的不等式；
(2)要求共获利不少于15600元，试写出装运A种苹果汽车x(辆)应满足的另一个不等式．
(1) 3x＋2(10－x)≥24； (2) 【解析】
1500x＋1800(10－x)≥15600
【解析】试题分析：（1）设x辆汽车运A种苹果，则有（10-x）辆汽车运B种苹果，根据题意可得不等关系：运出苹果超过24吨；②一次性获利超过15600元，根据不等关系列出不等式组；
（2）设x辆汽车运A种苹果，则有（10-x）辆汽车运B种苹果，根据题意可得不等关系：一次性获利超过15600... 方程3x＝12的解有___个，不等式3x＜12的解有____个．
1 无数
【解析】解方程3x=12，可得x=4，所以方程只有一个解，解不等式3x＜12，可得x＜4，知不等式的解有无数个.
故答案为：1；无数. 函数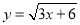
中自变量x的取值范围在数轴上表示正确的是（ ）
A．
B．
C．
D．
A．
【解析】
试题分析：由函数，得到3x+6≥0，解得：x≥﹣2，表示在数轴上，如图所示：
故选A． 如图，在△ABC中，∠C＝90°，∠B＝30°，AD平分∠CAB，交BC于点D，若CD＝1，则BD＝________．
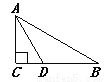
2
【解析】试题分析：根据角平分线性质求出∠BAD的度数，根据含30度角的直角三角形性质求出AD即可得BD．
∵∠C=90°，∠B=30°，∴∠CAB=60°，AD平分∠CAB，∴∠BAD=30°，∴BD=AD=2CD=2， 一个事件发生的概率不可能是( )
A. 0 B. 1 C.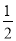 
D. 
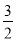
D
【解析】因为一个事件发生的概率不可能大于1,故选D.