题目内容
一个直角三角形的两条直角边长分别为6 cm和8 cm,那么这个直角三角形的斜边长为( )
A. 6 cm B. 8 cm C. 10 cm D. 24 cm
 C
【解析】根据勾股定理可以得出:斜边长==10cm.
故选:C.
C
【解析】根据勾股定理可以得出:斜边长==10cm.
故选:C.
练习册系列答案
相关题目
在□ABCD中,∠A∶∠B∶∠C∶∠D的值可以是( )
A.1∶2∶3∶4 B.1∶2∶2∶1
C.1∶1∶2∶2 D.2∶1∶2∶1
 D.
【解析】
试题解析:∵四边形ABCD是平行四边形,
∴∠A=∠C,∠B=∠D,AB∥CD,
∴∠B+∠C=180°,∠A+∠D=180°,
即∠A和∠C的数相等,∠B和∠D的数相等,且∠B+∠C=∠A+∠D,
故选D.
D.
【解析】
试题解析:∵四边形ABCD是平行四边形,
∴∠A=∠C,∠B=∠D,AB∥CD,
∴∠B+∠C=180°,∠A+∠D=180°,
即∠A和∠C的数相等,∠B和∠D的数相等,且∠B+∠C=∠A+∠D,
故选D. 函数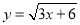 中自变量x的取值范围在数轴上表示正确的是( )
中自变量x的取值范围在数轴上表示正确的是( )
A.
B.
C.
D.
 A.
【解析】
试题分析:由函数,得到3x+6≥0,解得:x≥﹣2,表示在数轴上,如图所示:
故选A.
A.
【解析】
试题分析:由函数,得到3x+6≥0,解得:x≥﹣2,表示在数轴上,如图所示:
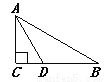
故选A. 如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,交BC于点D,若CD=1,则BD=________.
 2
【解析】试题分析:根据角平分线性质求出∠BAD的度数,根据含30度角的直角三角形性质求出AD即可得BD.
∵∠C=90°,∠B=30°,∴∠CAB=60°,AD平分∠CAB,∴∠BAD=30°,∴BD=AD=2CD=2,
2
【解析】试题分析:根据角平分线性质求出∠BAD的度数,根据含30度角的直角三角形性质求出AD即可得BD.
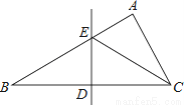
∵∠C=90°,∠B=30°,∴∠CAB=60°,AD平分∠CAB,∴∠BAD=30°,∴BD=AD=2CD=2, 如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB.若BE=2,则AE的长为( )
A. 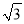 B. 1 C.
B. 1 C. 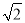 D. 2
D. 2
 B
【解析】试题解析:∵在△ABC中,∠B=30°,BC的垂直平分线交AB于E,BE=2,
∴BE=CE=2,
∴∠B=∠DCE=30°,
∵CE平分∠ACB,
∴∠ACB=2∠DCE=60°,∠ACE=∠DCE=30°,
∴∠A=180°-∠B-∠ACB=90°.
在Rt△CAE中,∵∠A=90°,∠ACE=30°,CE=2,
∴AE=CE=1.
...
B
【解析】试题解析:∵在△ABC中,∠B=30°,BC的垂直平分线交AB于E,BE=2,
∴BE=CE=2,
∴∠B=∠DCE=30°,
∵CE平分∠ACB,
∴∠ACB=2∠DCE=60°,∠ACE=∠DCE=30°,
∴∠A=180°-∠B-∠ACB=90°.
在Rt△CAE中,∵∠A=90°,∠ACE=30°,CE=2,
∴AE=CE=1.
... 计算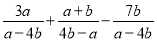 得( )
得( )
A. 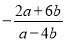 B.
B. 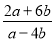 C.
C. 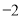 D. 2
D. 2
 D
【解析】试题分析:
=
=
=
=
=2.
故选D.
D
【解析】试题分析:
=
=
=
=
=2.
故选D. 若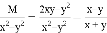 ,则M=___________.
,则M=___________.
 【解析】本题考查的是等式的性质
①将等号右边通分,得,比较等号左边的分式,不难得出. ②可以在等号两边都乘以后,化简右边即可.
①将等号右边通分,得,故;
②等号两边都乘得
【解析】本题考查的是等式的性质
①将等号右边通分,得,比较等号左边的分式,不难得出. ②可以在等号两边都乘以后,化简右边即可.
①将等号右边通分,得,故;
②等号两边都乘得 一个事件发生的概率不可能是( )
A. 0 B. 1 C. 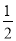 D.
D. 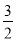
 D
【解析】因为一个事件发生的概率不可能大于1,故选D.
D
【解析】因为一个事件发生的概率不可能大于1,故选D. 下列事件中,是必然事件的为( )
A. 抛掷一枚质地均匀的硬币,落地后正面朝上
B. 江汉平原7月份某一天的最低气温是-2℃
C. 通常加热到100℃时,水沸腾
D. 打开电视,正在播放节目《男生女生向前冲》
 C
【解析】试题分析:根据必然事件就是一定发生的事件,即发生的概率是1的事件进行判断:
A,B,D选项,是可能发生也可能不发生的事件,属于不确定事件,不符合题意;是必然事件的是:通常加热到100℃时,水沸腾,符合题意。故选C。
C
【解析】试题分析:根据必然事件就是一定发生的事件,即发生的概率是1的事件进行判断:
A,B,D选项,是可能发生也可能不发生的事件,属于不确定事件,不符合题意;是必然事件的是:通常加热到100℃时,水沸腾,符合题意。故选C。 
