题目内容
计算: 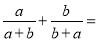 ________.
________.
 1
【解析】试题分析:原式=
=
=1.
故答案为:1.
1
【解析】试题分析:原式=
=
=1.
故答案为:1.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
A、B、C、D在同一平面内,从①AB∥CD;②AB=CD;③BC∥AD;④BC=AD;这四个条件中任选两个,能使四边形ABCD成为平行四边形的选法共有( )
A. 3种 B 4种 C 5种 D 6种
 B
【解析】试题分析:根据一组对边平行且相等、两组对边分别平行、两组对边分别相等来进行判定.则正确的选法为:①③、②④、①②、③④四种判定方法.
B
【解析】试题分析:根据一组对边平行且相等、两组对边分别平行、两组对边分别相等来进行判定.则正确的选法为:①③、②④、①②、③④四种判定方法. 如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,交BC于点D,若CD=1,则BD=________.
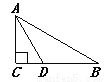
 2
【解析】试题分析:根据角平分线性质求出∠BAD的度数,根据含30度角的直角三角形性质求出AD即可得BD.
∵∠C=90°,∠B=30°,∴∠CAB=60°,AD平分∠CAB,∴∠BAD=30°,∴BD=AD=2CD=2,
2
【解析】试题分析:根据角平分线性质求出∠BAD的度数,根据含30度角的直角三角形性质求出AD即可得BD.
∵∠C=90°,∠B=30°,∴∠CAB=60°,AD平分∠CAB,∴∠BAD=30°,∴BD=AD=2CD=2, 计算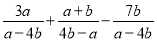 得( )
得( )
A. 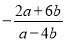 B.
B. 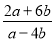 C.
C. 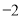 D. 2
D. 2
 D
【解析】试题分析:
=
=
=
=
=2.
故选D.
D
【解析】试题分析:
=
=
=
=
=2.
故选D. 若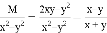 ,则M=___________.
,则M=___________.
 【解析】本题考查的是等式的性质
①将等号右边通分,得,比较等号左边的分式,不难得出. ②可以在等号两边都乘以后,化简右边即可.
①将等号右边通分,得,故;
②等号两边都乘得
【解析】本题考查的是等式的性质
①将等号右边通分,得,比较等号左边的分式,不难得出. ②可以在等号两边都乘以后,化简右边即可.
①将等号右边通分,得,故;
②等号两边都乘得 林业部门要考察某种幼树在一定条件下的移植成活率,下表是这种幼树在移植过程中的一组数据:
移植的 棵数n | 1000 | 1500 | 2500 | 4000 | 8000 | 15000 | 20000 | 30000 |
成活的 棵数m | 865 | 1356 | 2220 | 3500 | 7056 | 13170 | 17580 | 26430 |
成活的 频率 | 0.865 | 0.904 | 0.888 | 0.875 | 0.882 | 0.878 | 0.879 | 0.881 |
估计该种幼树在此条件下移植成活的概率为_________.
 0.88
【解析】因为(0.865+0.904+0.888+0.875+0.882+0.878+0.879+0.881)÷8≈0.88,所以这种幼树移植成活率的概率约为0.88,故答案为:0.88.
0.88
【解析】因为(0.865+0.904+0.888+0.875+0.882+0.878+0.879+0.881)÷8≈0.88,所以这种幼树移植成活率的概率约为0.88,故答案为:0.88. 一个事件发生的概率不可能是( )
A. 0 B. 1 C. 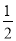 D.
D. 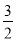
 D
【解析】因为一个事件发生的概率不可能大于1,故选D.
D
【解析】因为一个事件发生的概率不可能大于1,故选D. 如图所示,在?ABCD中,E为AD中点,CE交BA的延长线于F,若BC=2AB,∠FBC=70°,则∠EBC的度数为__度.
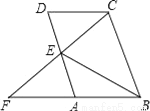
 35
【解析】∵ABCD,
∴AB=CD,DC∥AB,
∴∠ECD=∠EFA,
∵DE=AE,∠DEC=∠AEF,
∴△DEC≌△AEF,
∴DC=AF,
∴AB=AF.
∵BC=2AB,AB=AF,
∴BC=BF,
∴△FBC为等腰三角形,
再由△DEC≌△AEF,得EC=EF,
∴∠EBC=∠EBF=∠CBF=×70°=3...
35
【解析】∵ABCD,
∴AB=CD,DC∥AB,
∴∠ECD=∠EFA,
∵DE=AE,∠DEC=∠AEF,
∴△DEC≌△AEF,
∴DC=AF,
∴AB=AF.
∵BC=2AB,AB=AF,
∴BC=BF,
∴△FBC为等腰三角形,
再由△DEC≌△AEF,得EC=EF,
∴∠EBC=∠EBF=∠CBF=×70°=3... 如图,在?ABCD中,AB>AD,按以下步骤作图:以点A为圆心,小于AD的长为半径画弧,分别交AB、AD于点E、F;再分别以点E、F为圆心,大于 EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H,则下列结论中不能由条件推理得出的是( )
EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H,则下列结论中不能由条件推理得出的是( )

A. AG平分∠DAB B. AD=DH C. DH=BC D. CH=DH
 D
【解析】试题分析:由角平分线的作法,依题意可知AG平分∠DAB,A正确;∠DAH=∠BAH,又AB∥DC,所以∠BAH=∠ADH,所以,∠DAH=∠ADH,所以,AD=DH,又AD=BC,所以,DH=BC,B、C正确,故答案选D.
D
【解析】试题分析:由角平分线的作法,依题意可知AG平分∠DAB,A正确;∠DAH=∠BAH,又AB∥DC,所以∠BAH=∠ADH,所以,∠DAH=∠ADH,所以,AD=DH,又AD=BC,所以,DH=BC,B、C正确,故答案选D. 

