Question

6．已知一次函数y=kx+b与x轴交于点（2$\sqrt{3}$，0），且与x夹角为30°，求该一次函数的解析式．

Answer 1

分析 分类讨论：当∠OAB=30°时，先确定B（0，-2），然后利用待定系数法求出直线AB的解析式；当∠OAC=30°时，利用同样方法求出直线AC的解析式．

解答 解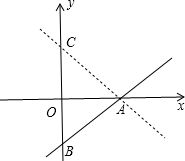：如图，A（2$\sqrt{3}$，0），
当∠OAB=30°时，OB=$\frac{\sqrt{3}}{3}$OA=2，则B（0，-2），
把（0，-2）、（2$\sqrt{3}$，0）代入y=kx+b得$\left\{\begin{array}{l}{b=-2}\\{2\sqrt{3}k+b=0}\end{array}\right.$，解得$\left\{\begin{array}{l}{k=\frac{\sqrt{3}}{3}}\\{b=-2}\end{array}\right.$，
此时一次函数解析式为y=$\frac{\sqrt{3}}{3}$x-2；
当∠OAC=30°时，OC=$\frac{\sqrt{3}}{3}$OA=2，则C（0，2），
把（0，2）、（2$\sqrt{3}$，0）代入y=kx+b得$\left\{\begin{array}{l}{b=2}\\{2\sqrt{3}k+b=0}\end{array}\right.$，解得$\left\{\begin{array}{l}{k=-\frac{\sqrt{3}}{3}}\\{b=2}\end{array}\right.$，
此时一次函数解析式为y=-$\frac{\sqrt{3}}{3}$x+2，
所以一次函数解析式为y=$\frac{\sqrt{3}}{3}$x-2或y=-$\frac{\sqrt{3}}{3}$x+2．

点评 本题考查了待定系数法求一次函数解析式：先设出函数的一般形式，如求一次函数的解析式时，先设y=kx+b；将自变量x的值及与它对应的函数值y的值代入所设的解析式，得到关于待定系数的方程或方程组；解方程或方程组，求出待定系数的值，进而写出函数解析式．