题目内容
11. 如图,已知DE∥BC,EF∥CD.
如图,已知DE∥BC,EF∥CD.(1)求证:AD2=AF•AB.
(2)若AD=BF,试求BF•AB的值.
分析 (1)根据平行线分线段成比例定理,得出AD:AB=AE:AC以及AF:AD=AE:AC,即可得出结论正确;
(2)设AF=x,则AB=BF+x=AD+x,由于AD2=AB•AF,于是得到AD2=x(AD+x)=AD•x+x2,证得x=$\frac{\sqrt{5}-1}{2}$AD,求得AB=$\frac{\sqrt{5}+1}{2}$AD,结论得到结论.
解答 证明:(1)∵DE∥BC,
∴AD:AB=AE:AC,
∵EF∥DC,
∴AF:AD=AE:AC,
∴AD:AB=AF:AD,
∴AD2=AB•AF;
(2)设AF=x,则AB=BF+x=AD+x,
∵AD2=AB•AF,
∴AD2=x(AD+x)=AD•x+x2,
∴x=$\frac{\sqrt{5}-1}{2}$AD,
∴AB=$\frac{\sqrt{5}+1}{2}$AD,
∴BF:AB=AD:AB=$\frac{\sqrt{5}-1}{2}$,
点评 此题主要考查了平行线分线段成比例定理,根据题意得出AD:AB=AE:AC以及AF:AD=AE:AC是解决问题的关键

练习册系列答案
相关题目
2.近似数0.5760精确到的位数是( )
| A. | 十分位 | B. | 百分位 | C. | 千分位 | D. | 万分位 |
1.绝对值不大于10.3的整数有( )
| A. | 10个 | B. | 11个 | C. | 20个 | D. | 21个 |
 平面上有△ACD与△BCE,其中AD与BE相交于P点,若AC=BC,CD=CE,∠ACB=∠ECD.
平面上有△ACD与△BCE,其中AD与BE相交于P点,若AC=BC,CD=CE,∠ACB=∠ECD.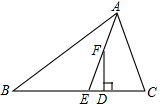 如图,在△ABC中,AE平分∠BAC,F为AE上一点,且FD⊥BC于点D,若∠C-∠B=40°,求∠EFD的度数.
如图,在△ABC中,AE平分∠BAC,F为AE上一点,且FD⊥BC于点D,若∠C-∠B=40°,求∠EFD的度数.