题目内容
15. 如图,在?ABCD中,AB=5,BC=8,BC边上的高AH=3,点P是边BC上的动点,以CP为半径的⊙C与边AD交于点E,F(点E在点F的左侧).
如图,在?ABCD中,AB=5,BC=8,BC边上的高AH=3,点P是边BC上的动点,以CP为半径的⊙C与边AD交于点E,F(点E在点F的左侧).(1)当⊙C经过点A时,求CP的长;
(2)连接AP,当AP∥CE时,求⊙C的半径及弦EF的长.
分析 (1)连接AC,由勾股定理求出BH=4,得出CH=4,由勾股定理求出CA,当⊙C经过点A时,CP=CA=5;
(2)先证明四边形APCE是平行四边形,得出CP=CE,证出四边形APCE是菱形,得出PA=CP,设PA=CP=x,则PH=4-x,由勾股定理得出方程,解方程求出半径;作CM⊥EF于M,则CM=AH=3,由垂径定理得出ME=MF=$\frac{1}{2}$EF,由勾股定理求出ME,即可得出EF的长.
解答 解:(1)连接AC,如图1所示: ∵AH⊥BC,
∵AH⊥BC,
∴∠AHB=∠AHC=90°,
∴BH=$\sqrt{A{B}^{2}-A{H}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴CH=BC-BH=4,
∴CA=$\sqrt{A{H}^{2}+C{H}^{2}}$=5,
当⊙C经过点A时,CP=CA=5;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,当AP∥CE时,四边形APCE是平行四边形,
∵CP=CE,
∴四边形APCE是菱形,
∴PA=CP,
设PA=CP=x,则PH=4-x,
在Rt△APH中,
由勾股定理得:AH2+PH2=PA2,
即32+(4-x)2=x2,
解得:x=$\frac{25}{8}$,
即⊙C的半径为$\frac{25}{8}$;
作CM⊥EF于M,如图2所示: 则CM=AH=3,ME=MF=$\frac{1}{2}$EF,
则CM=AH=3,ME=MF=$\frac{1}{2}$EF,
在Rt△CEM中,由勾股定理得:
ME=$\sqrt{C{E}^{2}-C{M}^{2}}$=$\sqrt{(\frac{25}{8})^{2}-{3}^{2}}$=$\frac{7}{8}$,
∴EF=2ME=$\frac{7}{4}$.
点评 本题考查了平行四边形的性质、勾股定理、垂径定理、平行四边形的判定方法、菱形的判定与性质等知识;本题综合性强,有一定难度.

 如图,在△ABC中,已知AB=AC,DE∥AC,试判断DB与DE的数量关系,并说明理由.
如图,在△ABC中,已知AB=AC,DE∥AC,试判断DB与DE的数量关系,并说明理由. 如图所示,点B,C,D在同一条直线上,且点A,B,C等分大圆,C,D,E等分小圆,连接BE,AD交于点M,求∠BMD的度数.
如图所示,点B,C,D在同一条直线上,且点A,B,C等分大圆,C,D,E等分小圆,连接BE,AD交于点M,求∠BMD的度数.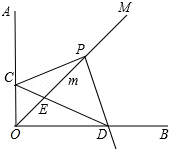 已知∠AOB=90°,OM是∠AOB的平分线,将一个直角三角板的直角顶点P放在射线OM上,OP=2,移动直角三角板,两边分别交射线OA,OB与点C,D.
已知∠AOB=90°,OM是∠AOB的平分线,将一个直角三角板的直角顶点P放在射线OM上,OP=2,移动直角三角板,两边分别交射线OA,OB与点C,D.