题目内容
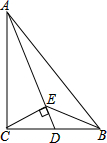 如图,Rt△ABC中,∠ACB=90°,D是BC的中点,CE⊥AD,垂足为E.
如图,Rt△ABC中,∠ACB=90°,D是BC的中点,CE⊥AD,垂足为E.(1)求证:CD2=DE•AD;
(2)求证:∠BED=∠ABC.
考点:相似三角形的判定与性质
专题:证明题
分析:(1)证明∠CED=∠ACB=90°,∠CDE=∠ADC,得到△CDE∽△ADC,列出比例式,化为等积式即可解决问题.
(2)运用(1)中的结论,证明△BDE∽△ADB,即可解决问题.
(2)运用(1)中的结论,证明△BDE∽△ADB,即可解决问题.
解答: 证明(1)∵CE⊥AD,
证明(1)∵CE⊥AD,
∴∠CED=∠ACB=90°,
∵∠CDE=∠ADC,
∴△CDE∽△ADC,
∴CD:AD=DE:CD,
∴CD2=DE•AD.
(2)∵D是BC的中点,
∴BD=CD;
∵CD2=DE•AD,
∴BD2=DE•AD
∴BD:AD=DE:BD;
又∵∠ADB=∠BDE,
∴△BDE∽△ADB,
∴∠BED=∠ABC.
 证明(1)∵CE⊥AD,
证明(1)∵CE⊥AD,∴∠CED=∠ACB=90°,
∵∠CDE=∠ADC,
∴△CDE∽△ADC,
∴CD:AD=DE:CD,
∴CD2=DE•AD.
(2)∵D是BC的中点,
∴BD=CD;
∵CD2=DE•AD,
∴BD2=DE•AD
∴BD:AD=DE:BD;
又∵∠ADB=∠BDE,
∴△BDE∽△ADB,
∴∠BED=∠ABC.
点评:该题主要考查了相似三角形的判定及其性质的应用问题;解题的关键是深入把握题意、大胆猜测推理、科学求解论证.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
已知三角形的三边长的比是1:
:
,那么这个三角形一定不是( )
| ||
| 2 |
| 1 | ||
|
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、不等边三角形 |
 如图,直线a、b被直线c所截,a∥b,∠1=121°,求∠3的度数.
如图,直线a、b被直线c所截,a∥b,∠1=121°,求∠3的度数.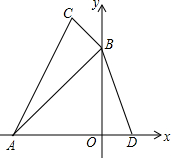 如图,在平面直角坐标系中,△ABC中点A(-3,0),B(0,3),C(-1,4),在x轴正半轴中有一个点D(1,0),连结BD,问:
如图,在平面直角坐标系中,△ABC中点A(-3,0),B(0,3),C(-1,4),在x轴正半轴中有一个点D(1,0),连结BD,问: