题目内容
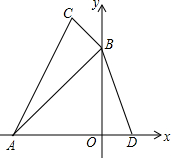 如图,在平面直角坐标系中,△ABC中点A(-3,0),B(0,3),C(-1,4),在x轴正半轴中有一个点D(1,0),连结BD,问:
如图,在平面直角坐标系中,△ABC中点A(-3,0),B(0,3),C(-1,4),在x轴正半轴中有一个点D(1,0),连结BD,问:(1)△ABC是
(2)在坐标轴上找一个点P,使得以B、D、P为顶点的△BDP与△ABC相似,则点P的坐标为
考点:相似三角形的判定,坐标与图形性质,勾股定理的逆定理
专题:
分析:(1)根据坐标可求得AB、AC、BC的长度,再利用勾股定理的逆定理可判断△ABC为直角三角形;
(2)分点P在x轴上时,只能在点D的左侧有∠BPD=90°或∠PBD=90°,点P在y轴上时,只能在B点的下方,同理分两种情况,再利用对应边成比例可求得其坐标.
(2)分点P在x轴上时,只能在点D的左侧有∠BPD=90°或∠PBD=90°,点P在y轴上时,只能在B点的下方,同理分两种情况,再利用对应边成比例可求得其坐标.
解答:解:(1)∵A(-3,0),B(0,3),C(-1,4),
∴AB2=32+32=18,AC2=(-1+3)2+42=20,BC2=(-1)2+(4-3)2=2,
∴AC2=AB2+BC2,
∴△ABC为直角三角形,
故答案为:直角;
(2)∵△ABC为直角三角形,
∴当△BDP与△ABC相似时,△BDP为直角三角形,且BD=
,
当P点在x轴上时,设P点坐标为(x,0),根据题意可知P点只能在D点的左侧,所以PD=1-x,此时有两种情况:
①当∠BPD=90°时,则有∠PBD=∠CAB,∴
=
,即
=
,解得x=0,此时P点为(0,0);
②当∠PBD=90°时,则有∠PDB=∠C,∴
=
,即
=
,解得x=-9,此时P点为(0,0);
当P点在y轴上时,设P点坐标为(0,y),根据题意可知P点只能在B点下方,所以PB=3-y,此时有两种情况:
①当∠BPD=90°时,则有∠PBD=∠CAB,∴
=
,即
=
,解得y=0,此时P点为(0,0);
②当∠PDB=90°时,则有∠PBD=∠CAB,∴
=
,即
=
,解得y=-
,此时P点为(0,
);
综上可知P点的坐标为:(0,0)或(-9,0)或(0,-
).
故答案为:(0,0)或(-9,0)或(0,-
).
∴AB2=32+32=18,AC2=(-1+3)2+42=20,BC2=(-1)2+(4-3)2=2,
∴AC2=AB2+BC2,
∴△ABC为直角三角形,
故答案为:直角;
(2)∵△ABC为直角三角形,
∴当△BDP与△ABC相似时,△BDP为直角三角形,且BD=
| 10 |
当P点在x轴上时,设P点坐标为(x,0),根据题意可知P点只能在D点的左侧,所以PD=1-x,此时有两种情况:
①当∠BPD=90°时,则有∠PBD=∠CAB,∴
| PD |
| BC |
| BD |
| AC |
| 1-x | ||
|
| ||
|
②当∠PBD=90°时,则有∠PDB=∠C,∴
| PD |
| AC |
| BD |
| BC |
| 1-x | ||
|
| ||
|
当P点在y轴上时,设P点坐标为(0,y),根据题意可知P点只能在B点下方,所以PB=3-y,此时有两种情况:
①当∠BPD=90°时,则有∠PBD=∠CAB,∴
| PB |
| AB |
| BD |
| AC |
| 3-y | ||
|
| ||
|
②当∠PDB=90°时,则有∠PBD=∠CAB,∴
| PB |
| AC |
| BD |
| AB |
| 3-y | ||
|
| ||
|
| 1 |
| 3 |
| 1 |
| 3 |
综上可知P点的坐标为:(0,0)或(-9,0)或(0,-
| 1 |
| 3 |
故答案为:(0,0)或(-9,0)或(0,-
| 1 |
| 3 |
点评:本题主要考查相似三角形的性质和勾股定理逆定理,掌握相似三角形的对应边成比例是解题的关键,注意分类讨论及方程思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
当x>2时,|1+
|等于( )
| (x-2)2 |
| A、1-x | B、x-1 |
| C、3-x | D、x-3 |
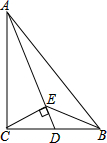 如图,Rt△ABC中,∠ACB=90°,D是BC的中点,CE⊥AD,垂足为E.
如图,Rt△ABC中,∠ACB=90°,D是BC的中点,CE⊥AD,垂足为E.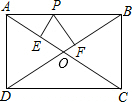 在矩形ABCD中,P为AB上的动点,PE⊥AC于E,PF⊥BD于F,求证:PE+PF为定值.
在矩形ABCD中,P为AB上的动点,PE⊥AC于E,PF⊥BD于F,求证:PE+PF为定值.