题目内容
抛物线与x轴交于点（1，0），（-3，0），则该抛物线可设为： ．
考点：二次函数的三种形式
专题：
分析：已知抛物线与x轴的两个交点，可以设该解析式为交点式．
解答：解：∵抛物线与x轴交于点（1，0），（-3，0），
∴设该抛物线解析式为：y=a（x-1）（x+3）（a≠0）．
故答案是：y=a（x-1）（x+3）（a≠0）．
∴设该抛物线解析式为：y=a（x-1）（x+3）（a≠0）．
故答案是：y=a（x-1）（x+3）（a≠0）．
点评：本题考查了抛物线的三种形式．交点式：y=a（x-x1）（x-x2）（a是常数，a≠0），该形式的优势是能直接根据解析式得到抛物线与x轴的两个交点坐标（x1，0），（x2，0）．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
在△ABC中，∠C=90°，BC=2，
=
，则边AC的长是（ ）
| BC |
| AB |
| 2 |
| 3 |
A、
| ||
| B、3 | ||
C、
| ||
D、
|
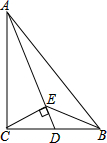如图，Rt△ABC中，∠ACB=90°，D是BC的中点，CE⊥AD，垂足为E．
如图所示，温度计上表示了摄氏温度（℃）与华氏温度（℉）的刻度．