题目内容
15.在四边形ABCD(凸四边形)中,AB=AD=BC,∠BAD=90°,连结对角线AC、当△ACD为等腰三角形时,通过画图探索可求得∠BCD所有可能的值为90°或135°.分析 根据题意可以画出相应的图形,得到∠BCD的度数,本题得以解决.
解答  解:如右图所示,
解:如右图所示,
当AD=AB=BC1时,在△AC1D中,AD=DC1,△AC1D是等腰三角形,
此时,∠BC1D=90°;
当AD=AB=BC2时,在△AC2D中,AD=AC2,△AC2D是等腰三角形,
则△ABC2是等边三角形,∠BAC2=∠BC2A=60°,
∵∠BAD=90°,
∴∠C2AD=30°,
∵AD=AC2,
∴∠AC2D=75°,
∴∠BC2D=∠BC2A+∠AC2D=60°+75°=135°,
故答案为:90°或135°.
点评 本题考查等腰三角形的性质,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
10.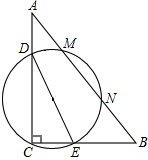 如图,在直角△ABC中,∠C=90°,BC=3,AC=4,D、E分别是AC、BC上的一点,且DE=3.若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为( )
如图,在直角△ABC中,∠C=90°,BC=3,AC=4,D、E分别是AC、BC上的一点,且DE=3.若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为( )
 如图,在直角△ABC中,∠C=90°,BC=3,AC=4,D、E分别是AC、BC上的一点,且DE=3.若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为( )
如图,在直角△ABC中,∠C=90°,BC=3,AC=4,D、E分别是AC、BC上的一点,且DE=3.若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为( )| A. | $\frac{8}{5}$ | B. | 2 | C. | $\frac{12}{5}$ | D. | $\frac{14}{5}$ |
7. 如图,△ABC与△BDE都是等边三角形,则AE与CD的大小关系为( )
如图,△ABC与△BDE都是等边三角形,则AE与CD的大小关系为( )
 如图,△ABC与△BDE都是等边三角形,则AE与CD的大小关系为( )
如图,△ABC与△BDE都是等边三角形,则AE与CD的大小关系为( )| A. | AE=CD | B. | AE>CD | C. | AE<CD | D. | 无法确定 |
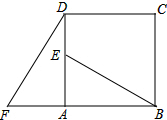 如图,四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如果AF=4,AB=7.
如图,四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如果AF=4,AB=7. 如图,长方形ABCD的面积为300cm2,长和宽的比为3:2.在此长方形内沿着边的方向能否并排裁出两个面积均为147cm2的圆(π取3),请通过计算说明理由.
如图,长方形ABCD的面积为300cm2,长和宽的比为3:2.在此长方形内沿着边的方向能否并排裁出两个面积均为147cm2的圆(π取3),请通过计算说明理由. 如图,Rt△AOB的直角边OA、OB分别在x轴正半轴和y轴正半轴上,OA=1,∠OBA=30°,将△AOB绕点A顺时针旋转,使AB的对应边AD恰好落在x轴上,若函数y=$\frac{k}{x}$(x>0)的图象经过点O的对应点C,则k的值为$\frac{3\sqrt{3}}{4}$.
如图,Rt△AOB的直角边OA、OB分别在x轴正半轴和y轴正半轴上,OA=1,∠OBA=30°,将△AOB绕点A顺时针旋转,使AB的对应边AD恰好落在x轴上,若函数y=$\frac{k}{x}$(x>0)的图象经过点O的对应点C,则k的值为$\frac{3\sqrt{3}}{4}$. 如图,已知函数y=-x+b的图象与x轴、y轴分别交于点A、B,与函数y=2x的图象交于点M,点M的横坐标为2,在x轴上有一点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=-x+b和y=2x的图象于点C,D.
如图,已知函数y=-x+b的图象与x轴、y轴分别交于点A、B,与函数y=2x的图象交于点M,点M的横坐标为2,在x轴上有一点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=-x+b和y=2x的图象于点C,D.