题目内容
5.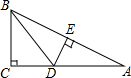 如图,在Rt△ABC中,∠C=90°,边AB的垂直平分线交AC于点D,交AB于点E.若BC=4,AC=8,则BD=( )
如图,在Rt△ABC中,∠C=90°,边AB的垂直平分线交AC于点D,交AB于点E.若BC=4,AC=8,则BD=( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 根据勾股定理求出AB的长,根据线段垂直平分线的性质得到DA=DB,DE⊥AB,AE=BE,根据△AED∽△ACB,得到比例式求出AD的长即可.
解答 解:∵∠C=90°,BC=4,AC=8,
∴AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=4$\sqrt{5}$,
∵DE是AB的垂直平分线,
∴DA=DB,DE⊥AB,AE=BE=2$\sqrt{5}$,
∴△AED∽△ACB,
∴$\frac{AE}{AC}$=$\frac{AD}{AB}$,即$\frac{2\sqrt{5}}{8}$=$\frac{AD}{4\sqrt{5}}$,
解得,AD=5,
∴BD=5,
故选:C.
点评 本题考查的是线段垂直平分线的性质、相似三角形的判定和性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
相关题目
11.已知点A(2,y1)、B(4,y2)都在反比例函数y=$\frac{k}{x}$(k<0)的图象上,则y1、y2的大小关系为( )
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 无法确定 |
12.估计$\sqrt{19}$的值在( )
| A. | 2和3之间 | B. | 3和4之间 | C. | 4和5之间 | D. | 5和6之间 |
10. 如图,四边形ABCD是⊙O的内接四边形,∠B=135°,则∠AOC的度数为( )
如图,四边形ABCD是⊙O的内接四边形,∠B=135°,则∠AOC的度数为( )
 如图,四边形ABCD是⊙O的内接四边形,∠B=135°,则∠AOC的度数为( )
如图,四边形ABCD是⊙O的内接四边形,∠B=135°,则∠AOC的度数为( )| A. | 45° | B. | 90° | C. | 100° | D. | 135° |
17.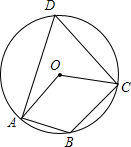 如图所示,四边形ABCD是⊙O的内接四边形,若∠AOC=120°,则∠ABC的度数是( )
如图所示,四边形ABCD是⊙O的内接四边形,若∠AOC=120°,则∠ABC的度数是( )
 如图所示,四边形ABCD是⊙O的内接四边形,若∠AOC=120°,则∠ABC的度数是( )
如图所示,四边形ABCD是⊙O的内接四边形,若∠AOC=120°,则∠ABC的度数是( )| A. | 100° | B. | 120° | C. | 140° | D. | 110° |
15. 如图,长4m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后的楼梯AC的长为( )
如图,长4m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后的楼梯AC的长为( )
 如图,长4m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后的楼梯AC的长为( )
如图,长4m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后的楼梯AC的长为( )| A. | 2$\sqrt{3}$m | B. | 2$\sqrt{6}$m | C. | (2$\sqrt{3}$-2)m | D. | (2$\sqrt{6}$-2)m |