题目内容
15. 如图,长4m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后的楼梯AC的长为( )
如图,长4m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后的楼梯AC的长为( )| A. | 2$\sqrt{3}$m | B. | 2$\sqrt{6}$m | C. | (2$\sqrt{3}$-2)m | D. | (2$\sqrt{6}$-2)m |
分析 先在Rt△ABD中利用正弦的定义计算出AD,然后在Rt△ACD中利用正弦的定义计算AC即可.
解答 解:在Rt△ABD中,∵sin∠ABD=$\frac{AD}{AB}$,
∴AD=4sin60°=2$\sqrt{3}$(m),
在Rt△ACD中,∵sin∠ACD=$\frac{AD}{AC}$,
∴AC=$\frac{2\sqrt{3}}{sin45°}$=2$\sqrt{6}$(m).
故选B.
点评 本题考查了解直角三角形的应用-坡度坡角:坡度是坡面的铅直高度h和水平宽度l的比,又叫做坡比,它是一个比值,反映了斜坡的陡峭程度,一般用i表示,常写成i=1:m的形式.把坡面与水平面的夹角α叫做坡角,坡度i与坡角α之间的关系为:i=tanα.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
10.下列四个数中,最大的一个数是( )
| A. | 2 | B. | $\sqrt{3}$ | C. | 0 | D. | -2 |
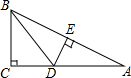
4.如图1,在等腰三角形ABC中,AB=AC=4,BC=7.如图2,在底边BC上取一点D,连结AD,使得∠DAC=∠ACD.如图3,将△ACD沿着AD所在直线折叠,使得点C落在点E处,连结BE,得到四边形ABED,则BE的长是( )


| A. | 4 | B. | $\frac{17}{4}$ | C. | 3$\sqrt{2}$ | D. | 2$\sqrt{5}$ |
5.如图所示,下列各三角形中的三个数之间均具有相同的规律,根据此规律,最后一个三角形中y与n之间的关系是( )


| A. | y=2n+1 | B. | y=2n+n | C. | y=2n+1+n | D. | y=2n+n+1 |
 如图,在Rt△ABC中,∠C=90°,边AB的垂直平分线交AC于点D,交AB于点E.若BC=4,AC=8,则BD=( )
如图,在Rt△ABC中,∠C=90°,边AB的垂直平分线交AC于点D,交AB于点E.若BC=4,AC=8,则BD=( )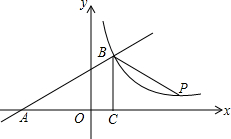 如图,一次函数y=kx+b的图象与x轴交于点A,与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点B(2,n),过点B作BC⊥x轴于点C,点P(3n-4,1)是该反比例函数图象上的一点,且∠PBC=∠ABC,求反比例函数和一次函数的表达式.
如图,一次函数y=kx+b的图象与x轴交于点A,与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点B(2,n),过点B作BC⊥x轴于点C,点P(3n-4,1)是该反比例函数图象上的一点,且∠PBC=∠ABC,求反比例函数和一次函数的表达式. 如图,将两个形状和大小都相同的杯子叠放在一起,则该实物图的主视图为( )
如图,将两个形状和大小都相同的杯子叠放在一起,则该实物图的主视图为( )


