题目内容
10. 如图,四边形ABCD是⊙O的内接四边形,∠B=135°,则∠AOC的度数为( )
如图,四边形ABCD是⊙O的内接四边形,∠B=135°,则∠AOC的度数为( )| A. | 45° | B. | 90° | C. | 100° | D. | 135° |
分析 由圆内接四边形的性质先求得∠D的度数,然后依据圆周角定理求解即可.
解答 解:∵四边形ABCD是⊙O的内接四边形,
∴∠B+∠D=180°.
∴∠D=180°-135°=45°.
∴∠AOC=90°.
故选;B.
点评 本题主要考查的是圆内接四边形的性质、圆周角定理的应用,求得∠D的度数是解题的关键.

练习册系列答案
相关题目
16.下列运算正确的是( )
| A. | a2•a3=a6 | B. | 5a-2a=3a2 | C. | (a3)4=a12 | D. | (x+y)2=x2+y2 |
15.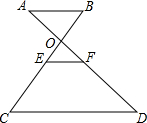 如图,AB∥EF∥CD,BC、AD相交于点O,F是AD的中点,则下列结论中错误的是( )
如图,AB∥EF∥CD,BC、AD相交于点O,F是AD的中点,则下列结论中错误的是( )
 如图,AB∥EF∥CD,BC、AD相交于点O,F是AD的中点,则下列结论中错误的是( )
如图,AB∥EF∥CD,BC、AD相交于点O,F是AD的中点,则下列结论中错误的是( )| A. | $\frac{AO}{AD}$=$\frac{BO}{BC}$ | B. | $\frac{OB}{CE}$=$\frac{OA}{DF}$ | C. | $\frac{EF}{CD}$=$\frac{OE}{BE}$ | D. | $\frac{2BE}{AD}$=$\frac{OE}{OF}$ |
19. 如图,把一张矩形纸片ABCD沿EF折叠后,点A落在CD边上的点A′处,点B落在点B′处,若∠2=40°,则图中∠1的度数为( )
如图,把一张矩形纸片ABCD沿EF折叠后,点A落在CD边上的点A′处,点B落在点B′处,若∠2=40°,则图中∠1的度数为( )
 如图,把一张矩形纸片ABCD沿EF折叠后,点A落在CD边上的点A′处,点B落在点B′处,若∠2=40°,则图中∠1的度数为( )
如图,把一张矩形纸片ABCD沿EF折叠后,点A落在CD边上的点A′处,点B落在点B′处,若∠2=40°,则图中∠1的度数为( )| A. | 115° | B. | 120° | C. | 130° | D. | 140° |
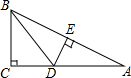 如图,在Rt△ABC中,∠C=90°,边AB的垂直平分线交AC于点D,交AB于点E.若BC=4,AC=8,则BD=( )
如图,在Rt△ABC中,∠C=90°,边AB的垂直平分线交AC于点D,交AB于点E.若BC=4,AC=8,则BD=( )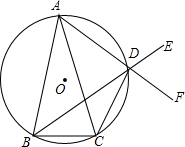 如图,已知⊙O是△ABC的外接圆,AB=AC,D是劣弧AC上的点(不与点A、C重合),延长BD至E.
如图,已知⊙O是△ABC的外接圆,AB=AC,D是劣弧AC上的点(不与点A、C重合),延长BD至E.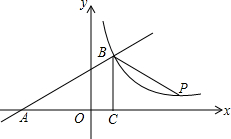 如图,一次函数y=kx+b的图象与x轴交于点A,与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点B(2,n),过点B作BC⊥x轴于点C,点P(3n-4,1)是该反比例函数图象上的一点,且∠PBC=∠ABC,求反比例函数和一次函数的表达式.
如图,一次函数y=kx+b的图象与x轴交于点A,与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点B(2,n),过点B作BC⊥x轴于点C,点P(3n-4,1)是该反比例函数图象上的一点,且∠PBC=∠ABC,求反比例函数和一次函数的表达式.