题目内容
7.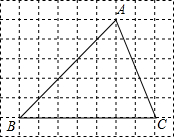 在正方形网格中,△ABC的位置如图所示,则cos∠B的值为( )
在正方形网格中,△ABC的位置如图所示,则cos∠B的值为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | 1 |
分析 cos∠B的值可以转化为直角三角形的边的比的问题,因而过点A作AD垂直于BC的延长线于点D.在Rt△ABD中根据三角函数的定义求解.
解答  解:作AD⊥BC的延长线于点D.
解:作AD⊥BC的延长线于点D.
在Rt△ABD中,BD=AD,则AB=$\sqrt{2}$BD.
故cos∠B=$\frac{\sqrt{2}}{2}$.
故选A.
点评 本题考查锐角三角函数的概念:在直角三角形中,正弦等于对边比斜边;余弦等于邻边比斜边;正切等于对边比邻边.

练习册系列答案
相关题目
17.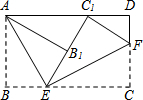 将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,BE=1,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则EC的长为( )
将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,BE=1,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则EC的长为( )
 将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,BE=1,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则EC的长为( )
将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,BE=1,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则EC的长为( )| A. | $\sqrt{3}$ | B. | 2 | C. | 3 | D. | 2$\sqrt{3}$ |
18.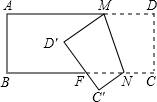 如图所示,把一长方形纸片沿MN折叠后,点D,C分别落在D′,C′的位置.若∠AMD′=35°,则∠NFD′等于( )
如图所示,把一长方形纸片沿MN折叠后,点D,C分别落在D′,C′的位置.若∠AMD′=35°,则∠NFD′等于( )
 如图所示,把一长方形纸片沿MN折叠后,点D,C分别落在D′,C′的位置.若∠AMD′=35°,则∠NFD′等于( )
如图所示,把一长方形纸片沿MN折叠后,点D,C分别落在D′,C′的位置.若∠AMD′=35°,则∠NFD′等于( )| A. | 115° | B. | 125° | C. | 135° | D. | 145° |
15.若a-b=5,ab=3,则(a+1)(b-1)的结果是( )
| A. | 5 | B. | 3 | C. | -3 | D. | -5 |
2.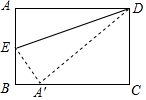 一张矩形纸片ABCD,AD=5cm,AB=3cm,将纸片沿ED折叠,A点刚好落在BC边上的A'处,如图,这时AE的长应该是( )
一张矩形纸片ABCD,AD=5cm,AB=3cm,将纸片沿ED折叠,A点刚好落在BC边上的A'处,如图,这时AE的长应该是( )
 一张矩形纸片ABCD,AD=5cm,AB=3cm,将纸片沿ED折叠,A点刚好落在BC边上的A'处,如图,这时AE的长应该是( )
一张矩形纸片ABCD,AD=5cm,AB=3cm,将纸片沿ED折叠,A点刚好落在BC边上的A'处,如图,这时AE的长应该是( )| A. | $\frac{5}{3}$cm | B. | $\frac{4}{3}$cm | C. | $\frac{3}{2}$cm | D. | $\frac{7}{5}$cm |
12.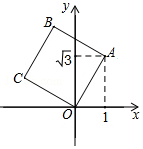 如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1,$\sqrt{3}$),则点B的坐标为( )
如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1,$\sqrt{3}$),则点B的坐标为( )
 如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1,$\sqrt{3}$),则点B的坐标为( )
如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1,$\sqrt{3}$),则点B的坐标为( )| A. | (1-$\sqrt{3}$,$\sqrt{3}$+1) | B. | (-$\sqrt{3}$,$\sqrt{3}$+1) | C. | (-1,$\sqrt{3}$+1) | D. | (-1,$\sqrt{3}$) |
19.如果将抛物线y=x2+2向右平移1个单位,那么所得新抛物线的表达式是( )
| A. | y=x2+3 | B. | y=(x-1)2+2 | C. | y=(x+1)2+2 | D. | y=x2+1 |
16.在平面直角坐标系内,将△ABC进行平移后得到△A′B′C′,其中点A(2,1)的对应点A′为(-2,-1),那么△ABC是( )
| A. | 向右平移了4个单位长度 | B. | 向左平移了4个单位长度 | ||
| C. | 向上平移了4个单位长度 | D. | 向下平移了4个单位长度 |
17.圆的周长C与半径r之间的函数关系式C=2πr中,变量是( )
| A. | C | B. | 2π | C. | r | D. | C和r |