题目内容
10．在函数y=$\frac{\sqrt{3x+6}}{x}$中，自变量x的取值范围是（ ）| A． | x≥-2 | B． | x＞-0 | C． | x≥-2且x≠0 | D． | x＞-2且x≠0 |
分析 根据被开方数大于等于0，分母不等于0列式计算即可得解．
解答 解：由题意得，3x+6≥0且x≠0，
解得x≥-2且x≠0．
故选C．
点评 本题考查了函数自变量的范围，一般从三个方面考虑：
（1）当函数表达式是整式时，自变量可取全体实数；（2）当函数表达式是分式时，考虑分式的分母不能为0；（3）当函数表达式是二次根式时，被开方数非负．
练习册系列答案
相关题目
20．下列调查的样本选取方式，最具有代表性的是（ ）
| A． | 在青少年中调查年度最受欢迎的男歌手 | |
| B． | 了解班上学生的睡眠时间．调查班上学号为双号的学生的睡眠时间 | |
| C． | 为了了解你所在学校的学生每天的上网时间，向八年级的同学进行调查 | |
| D． | 对某市的出租司机进行体检，以此反映该市市民的健康状况 |
1．
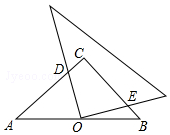如图，在等腰直角△ABC中，∠C=90°，点O是AB的中点，且AB=$\sqrt{6}$，将一块直角三角板的直角顶点放在点O处，始终保持该直角三角板的两直角边分别与AB、BC相交，交点分别为D、E，则CD+CE=（ ）
如图，在等腰直角△ABC中，∠C=90°，点O是AB的中点，且AB=$\sqrt{6}$，将一块直角三角板的直角顶点放在点O处，始终保持该直角三角板的两直角边分别与AB、BC相交，交点分别为D、E，则CD+CE=（ ）| A． | $\sqrt{3}$ | B． | $\sqrt{2}$ | C． | 2 | D． | $\sqrt{6}$ |
18．
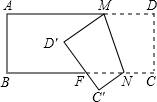如图所示，把一长方形纸片沿MN折叠后，点D，C分别落在D′，C′的位置．若∠AMD′=35°，则∠NFD′等于（ ）
如图所示，把一长方形纸片沿MN折叠后，点D，C分别落在D′，C′的位置．若∠AMD′=35°，则∠NFD′等于（ ）| A． | 115° | B． | 125° | C． | 135° | D． | 145° |
5．若-4≤x≤3，化简$\sqrt{{x}^{2}+8x+16}$-$\sqrt{{x}^{2}-6x+9}$的结果为（ ）
| A． | 2x+1 | B． | -2x-1 | C． | 1 | D． | 7 |
15．若a-b=5，ab=3，则（a+1）（b-1）的结果是（ ）
| A． | 5 | B． | 3 | C． | -3 | D． | -5 |
2．
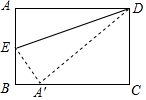一张矩形纸片ABCD，AD=5cm，AB=3cm，将纸片沿ED折叠，A点刚好落在BC边上的A'处，如图，这时AE的长应该是（ ）
一张矩形纸片ABCD，AD=5cm，AB=3cm，将纸片沿ED折叠，A点刚好落在BC边上的A'处，如图，这时AE的长应该是（ ）| A． | $\frac{5}{3}$cm | B． | $\frac{4}{3}$cm | C． | $\frac{3}{2}$cm | D． | $\frac{7}{5}$cm |
19．如果将抛物线y=x2+2向右平移1个单位，那么所得新抛物线的表达式是（ ）
| A． | y=x2+3 | B． | y=（x-1）2+2 | C． | y=（x+1）2+2 | D． | y=x2+1 |
20．不等式3x-5＜3+x的解集是（ ）
| A． | x＞4 | B． | x＜-1 | C． | x＜4 | D． | x＜$\frac{1}{2}$ |