题目内容
6.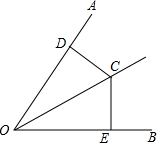 如图,OC是∠AOB的角平分线.D,E分别是OA,OB上的点,则下列条件中不能判定△OCD与△OCE全等的是( )
如图,OC是∠AOB的角平分线.D,E分别是OA,OB上的点,则下列条件中不能判定△OCD与△OCE全等的是( )| A. | ∠OCD=∠OCE | B. | CD⊥OA,CE⊥OB | C. | OD=OE | D. | CD=CE |
分析 利用全等三角形的判定定理解答即可.
解答 解:$\left\{\begin{array}{l}{∠DOC=∠EOC}\\{OC=OC}\\{∠OCD=∠OCE}\end{array}\right.$,
∴△OCD≌△OCE(ASA),A能判定△OCD与△OCE全等;
当CD⊥OA,CE⊥OB时,由AAS得到△OCD≌△OCE,B能判定△OCD与△OCE全等;
当OD=OE时,由SAS得到△OCD≌△OCE,C能判定△OCD与△OCE全等;
D不能判定△OCD与△OCE全等;
故选:D.
点评 本题考查的是角平分线的定义、全等三角形的判定,掌握全等三角形的判定定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16. 如图,在△ABC中,E、F分别是AD、CE边的中点,且S△BEF=3cm2,则S△ABC为( )
如图,在△ABC中,E、F分别是AD、CE边的中点,且S△BEF=3cm2,则S△ABC为( )
 如图,在△ABC中,E、F分别是AD、CE边的中点,且S△BEF=3cm2,则S△ABC为( )
如图,在△ABC中,E、F分别是AD、CE边的中点,且S△BEF=3cm2,则S△ABC为( )| A. | 6 cm2 | B. | 8 cm2 | C. | 10 cm2 | D. | 12 cm2 |
17.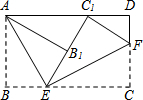 将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,BE=1,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则EC的长为( )
将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,BE=1,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则EC的长为( )
 将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,BE=1,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则EC的长为( )
将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,BE=1,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则EC的长为( )| A. | $\sqrt{3}$ | B. | 2 | C. | 3 | D. | 2$\sqrt{3}$ |
14.下列方程是二元一次方程的是( )
| A. | x+2=1 | B. | x2+2y=2 | C. | y2+y=4 | D. | x+5y=0 |
1.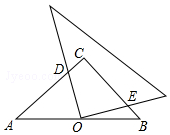 如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,且AB=$\sqrt{6}$,将一块直角三角板的直角顶点放在点O处,始终保持该直角三角板的两直角边分别与AB、BC相交,交点分别为D、E,则CD+CE=( )
如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,且AB=$\sqrt{6}$,将一块直角三角板的直角顶点放在点O处,始终保持该直角三角板的两直角边分别与AB、BC相交,交点分别为D、E,则CD+CE=( )
 如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,且AB=$\sqrt{6}$,将一块直角三角板的直角顶点放在点O处,始终保持该直角三角板的两直角边分别与AB、BC相交,交点分别为D、E,则CD+CE=( )
如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,且AB=$\sqrt{6}$,将一块直角三角板的直角顶点放在点O处,始终保持该直角三角板的两直角边分别与AB、BC相交,交点分别为D、E,则CD+CE=( )| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{6}$ |
11.已知a+b=5,ab=4,则a-b的值为( )
| A. | 9 | B. | 3 | C. | -3 | D. | ±3 |
18.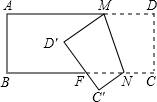 如图所示,把一长方形纸片沿MN折叠后,点D,C分别落在D′,C′的位置.若∠AMD′=35°,则∠NFD′等于( )
如图所示,把一长方形纸片沿MN折叠后,点D,C分别落在D′,C′的位置.若∠AMD′=35°,则∠NFD′等于( )
 如图所示,把一长方形纸片沿MN折叠后,点D,C分别落在D′,C′的位置.若∠AMD′=35°,则∠NFD′等于( )
如图所示,把一长方形纸片沿MN折叠后,点D,C分别落在D′,C′的位置.若∠AMD′=35°,则∠NFD′等于( )| A. | 115° | B. | 125° | C. | 135° | D. | 145° |
15.若a-b=5,ab=3,则(a+1)(b-1)的结果是( )
| A. | 5 | B. | 3 | C. | -3 | D. | -5 |
16.在平面直角坐标系内,将△ABC进行平移后得到△A′B′C′,其中点A(2,1)的对应点A′为(-2,-1),那么△ABC是( )
| A. | 向右平移了4个单位长度 | B. | 向左平移了4个单位长度 | ||
| C. | 向上平移了4个单位长度 | D. | 向下平移了4个单位长度 |