题目内容
2.已知x,y为实数,且y=$\sqrt{1-8x}$+$\sqrt{8x-1}$$+\frac{1}{2}$,则$\sqrt{xy}$的平方根等于±$\frac{1}{2}$.分析 首先根据二次根式有意义的条件:被开方数是非负数求得x的值,然后求得y的值,然后求解.
解答 解:根据题意得1-8x=0,
解得:x=$\frac{1}{8}$,
则y=$\frac{1}{2}$.
则$\sqrt{xy}$=$\sqrt{\frac{1}{8}×\frac{1}{2}}$=$\frac{1}{4}$,
则$\sqrt{xy}$的平方根是±$\frac{1}{2}$.
点评 本题考查了二次根式有意义的条件,理解$\sqrt{a}$有意义的条件是a≥0是关键.

练习册系列答案
相关题目
12. 如图所示:被圆圈盖住的点的坐标可能是( )
如图所示:被圆圈盖住的点的坐标可能是( )
 如图所示:被圆圈盖住的点的坐标可能是( )
如图所示:被圆圈盖住的点的坐标可能是( )| A. | (5,2) | B. | (-6,3) | C. | (-4,-6) | D. | (3,-4) |
14.程大位《直指算法统宗》:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚得几丁.意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完.试问大、小和尚各多少人?设大和尚有x人,依题意列方程得( )
| A. | $\frac{x}{3}$+3(100-x)=100 | B. | $\frac{x}{3}$-3(100-x)=100 | C. | 3x+$\frac{100-x}{3}$=100 | D. | 3x-$\frac{100-x}{3}$=100 |
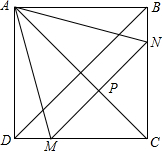 如图,在正方形ABCD中,有一个△AMN,MA=NA,M、N分别在DC、BC上,连接BD、AC,若∠DAM=15°,则下列说法中:?
如图,在正方形ABCD中,有一个△AMN,MA=NA,M、N分别在DC、BC上,连接BD、AC,若∠DAM=15°,则下列说法中:?