题目内容
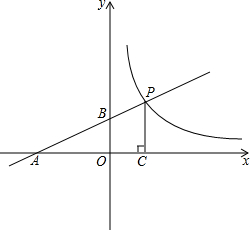 如图,直线y=
如图,直线y=| 1 |
| 2 |
| k |
| x |
(1)求双曲线的解析式;
(2)观察图象直接写出不等式
| 1 |
| 2 |
| k |
| x |
(3)在(1)中所求的双曲线上是否存在点Q(m,n)(其中m>0),作QH⊥x轴于H,使得△QCH与△AOB相似?若存在,请求出Q点坐标;若不存在,请说明理由.
考点:反比例函数综合题
专题:
分析:(1)把点P(2,y0)代入直线y=
x+2求出y0的值,再代入反比例函数y=
求出k的值即可;
(2)直接根据函数的图象即可得出不等式的解集;
(3)先求出A点坐标,再根据△QCH∽△AOB即可得出Q点的坐标.
| 1 |
| 2 |
| k |
| x |
(2)直接根据函数的图象即可得出不等式的解集;
(3)先求出A点坐标,再根据△QCH∽△AOB即可得出Q点的坐标.
解答:解:(1)∵点P(2,y0)在直线y=
x+2上,
∴y0=
×2+2=3,
∴点P(2,3),
∴3=
,
解得k=6,
∴双曲线的解析式为y=
(x>0);
(2)∵由函数图象可知,当x>2时,一次函数的图象在反比例函数图象的上方,
∴不等式
x+2>
的解集为:x>2;
(3)∵A(-4,0),B(0,2),
∴OA=4,OB=2,
∵Q(m,n)在双曲线y=
(x>0)上,
∴n=
,
当△AOB∽△CHQ时,
=
,即
=
,解得m=1+
或
m=1-
(舍去),
∴Q(1+
,
);
当△AOB∽△QHC时,
=
,即
=
,即m2-2m+3=0,
∵△<0,
∴此种情况不存在.
∴Q(1+
,
).
| 1 |
| 2 |
∴y0=
| 1 |
| 2 |
∴点P(2,3),
∴3=
| k |
| 2 |
解得k=6,
∴双曲线的解析式为y=
| 6 |
| x |
(2)∵由函数图象可知,当x>2时,一次函数的图象在反比例函数图象的上方,
∴不等式
| 1 |
| 2 |
| k |
| x |
(3)∵A(-4,0),B(0,2),

∴OA=4,OB=2,
∵Q(m,n)在双曲线y=
| 6 |
| x |
∴n=
| 6 |
| m |
当△AOB∽△CHQ时,
| AO |
| CH |
| OB |
| HQ |
| 4 |
| m-2 |
| 2 | ||
|
| 13 |
m=1-
| 13 |
∴Q(1+
| 13 |
| ||
| 2 |
当△AOB∽△QHC时,
| AO |
| QH |
| OB |
| CH |
| 4 | ||
|
| 2 |
| 2-m |
∵△<0,
∴此种情况不存在.
∴Q(1+
| 13 |
| ||
| 2 |
点评:本题考查的是反比例函数的综合题,考查了用待定系数法求函数的解析式、相似三角形的判定与性质等知识点,难度适中.

练习册系列答案
相关题目
数据3,-1,0,2,-1的中位数是( )
| A、-1 | B、0 | C、2 | D、3 |
 在平面直角坐标系中,点A1,A2,A3,…和B1,B2,B3,…分别在直线y=kx+b和x轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果A1(1,1),A2(
在平面直角坐标系中,点A1,A2,A3,…和B1,B2,B3,…分别在直线y=kx+b和x轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果A1(1,1),A2(| 7 |
| 2 |
| 3 |
| 2 |
A、(
| ||
B、(
| ||
C、(
| ||
D、(
|
 (1)如图,在1×1的正方形网格中,
(1)如图,在1×1的正方形网格中,