题目内容
如图1、2,已知四边形ABCD为正方形,在射线AC上有一动点P,作PE⊥AD(或延长线)于E,作PF⊥DC(或延长线)于F,作射线BP交EF于G.
(1)在图1中,设正方形ABCD的边长为2,四边形ABFE的面积为y,AP=x,求y关于x的函数表达式;
(2)结论:GB⊥EF对图1,图2都是成立的,请任选一图形给出证明;
(3)请根据图2证明:△FGC∽△PFB.
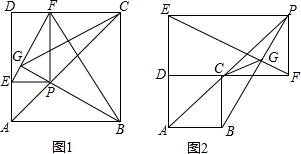
(1)在图1中,设正方形ABCD的边长为2,四边形ABFE的面积为y,AP=x,求y关于x的函数表达式;
(2)结论:GB⊥EF对图1,图2都是成立的,请任选一图形给出证明;
(3)请根据图2证明:△FGC∽△PFB.

考点:四边形综合题
专题:压轴题
分析:(1)根据题意得出S四边形ABFE=4-
ED×DF-
BC×FC进而得出答案;
(2)首先利用正方形的性质进而证明△FPE≌△BHP(SAS),即可得出△FPG∽△BPH,求出即可;
(3)首先得出△DPC≌△BPC(SAS),进而利用相似三角形的判定得出△FGC∽△PFB.
| 1 |
| 2 |
| 1 |
| 2 |
(2)首先利用正方形的性质进而证明△FPE≌△BHP(SAS),即可得出△FPG∽△BPH,求出即可;
(3)首先得出△DPC≌△BPC(SAS),进而利用相似三角形的判定得出△FGC∽△PFB.
解答:(1)解:∵PE⊥AD,PF⊥DC,
∴四边形EPFD是矩形,
∵AP=x,
∴AE=EP=DF=
x,
DE=PF=FC=2-
x,
∴S四边形ABFE=4-
ED•DF-
BC•FC
=4-
×
x(2-
x)-
×2×(2-
x)
=
x2+2;
(2)证明:如图1,延长FP交AB于H,
∵PF⊥DC,PE⊥AD,
∴PF⊥PE,PH⊥HB,
即∠BHP=90°,
∵四边形ABCD是正方形,
∴AC平分∠DAB,
∴可得PF=FC=HB,EP=PH,
在△FPE与△BHP中
,
∴△FPE≌△BHP(SAS),
∴∠PFE=∠PBH,
又∵∠FPG=∠BPH,
∴△FPG∽△BPH,
∴∠FGP=∠BHP=90°,
即GB⊥EF;
(3)证明:如图2,连接PD,∵GB⊥EF,
∴∠BPF=∠CFG①,
在△DPC和△BPC中
,
∴△DPC≌△BPC(SAS),
∴PD=PB,
而PD=EF,∴EF=PB,
又∵GB⊥EF,
∴PF2=FG•EF,
∴PF2=FG•PB,
而PF=FC,
∴PF•FC=FG•PB,
∴
=
②,
∴由①②得△FGC∽△PFB.
∴四边形EPFD是矩形,
∵AP=x,
∴AE=EP=DF=
| ||
| 2 |
DE=PF=FC=2-
| ||
| 2 |

∴S四边形ABFE=4-
| 1 |
| 2 |
| 1 |
| 2 |
=4-
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
=
| 1 |
| 4 |
(2)证明:如图1,延长FP交AB于H,
∵PF⊥DC,PE⊥AD,
∴PF⊥PE,PH⊥HB,
即∠BHP=90°,
∵四边形ABCD是正方形,
∴AC平分∠DAB,
∴可得PF=FC=HB,EP=PH,
在△FPE与△BHP中
|
∴△FPE≌△BHP(SAS),
∴∠PFE=∠PBH,
又∵∠FPG=∠BPH,
∴△FPG∽△BPH,
∴∠FGP=∠BHP=90°,
即GB⊥EF;
(3)证明:如图2,连接PD,∵GB⊥EF,
∴∠BPF=∠CFG①,
在△DPC和△BPC中
|

∴△DPC≌△BPC(SAS),
∴PD=PB,
而PD=EF,∴EF=PB,
又∵GB⊥EF,
∴PF2=FG•EF,
∴PF2=FG•PB,
而PF=FC,
∴PF•FC=FG•PB,
∴
| PF |
| PB |
| FG |
| FC |
∴由①②得△FGC∽△PFB.
点评:此题主要考查了正方形的性质以及全等三角形的判定和相似三角形的判定与性质等知识,熟练应用正方形的性质得出对应角以及对应边的关系是解题关键.

练习册系列答案
相关题目
 如图把一块含有30°角的直角三角板两个顶点放在一把直尺的对边上,如果∠1=25°,那么∠2的度数为( )
如图把一块含有30°角的直角三角板两个顶点放在一把直尺的对边上,如果∠1=25°,那么∠2的度数为( )| A、25° | B、35° |
| C、45° | D、55° |
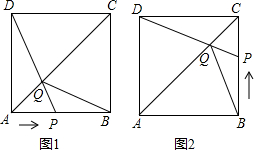 如图,在边长为1的正方形ABCD中,动点P从点A出发,沿着折线A→B→C的路线向终点C运动,连结DP交AC于点Q,连结BQ.
如图,在边长为1的正方形ABCD中,动点P从点A出发,沿着折线A→B→C的路线向终点C运动,连结DP交AC于点Q,连结BQ.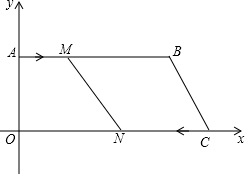 如图,在平面直角坐标系中,四边形AOCB的点O在坐标原点上,点A在y轴上,AB∥OC,点B的坐标为(15,8),点C的坐标为(21,0),动点M从点A沿AB方向以每秒1个长度单位的速度运动,动点N从C点沿CO的方向以每秒2个长度单位的速度运动.点M、N同时出发,一点到达终点时,另一点也停止运动,设运动时间为t秒.
如图,在平面直角坐标系中,四边形AOCB的点O在坐标原点上,点A在y轴上,AB∥OC,点B的坐标为(15,8),点C的坐标为(21,0),动点M从点A沿AB方向以每秒1个长度单位的速度运动,动点N从C点沿CO的方向以每秒2个长度单位的速度运动.点M、N同时出发,一点到达终点时,另一点也停止运动,设运动时间为t秒.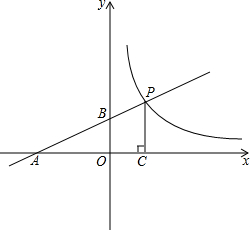 如图,直线
如图,直线