题目内容
 在平面直角坐标系中,点A1,A2,A3,…和B1,B2,B3,…分别在直线y=kx+b和x轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果A1(1,1),A2(
在平面直角坐标系中,点A1,A2,A3,…和B1,B2,B3,…分别在直线y=kx+b和x轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果A1(1,1),A2(| 7 |
| 2 |
| 3 |
| 2 |
A、(
| ||
B、(
| ||
C、(
| ||
D、(
|
考点:一次函数图象上点的坐标特征,等腰直角三角形
专题:规律型
分析:先利用待定系数法确定一次函数解析式为y=
x+
,再作A1C⊥x轴于C,A2D⊥x轴于D,A3H⊥x轴于H,根据等腰直角三角形的性质得A1C=1,A2D=
,设A3H=t,于是可表示出A3的坐标为(5+t,t),接着把A3(5+t,t)代入y=
x+
可解得t=
,所以点A3的纵坐标为(
)2,同理可得点A4的纵坐标为(
)3,按此规律可得点An的纵坐标为(
)n-1.
| 1 |
| 5 |
| 4 |
| 5 |
| 3 |
| 2 |
| 1 |
| 5 |
| 4 |
| 5 |
| 9 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
解答: 解:把A1(1,1),A2(
解:把A1(1,1),A2(
,
)代入y=kx+b得
,解得
,
所以一次函数解析式为y=
x+
,
作A1C⊥x轴于C,A2D⊥x轴于D,A3H⊥x轴于H,如图,
则A1C=1,A2D=
,设A3H=t,
∵△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,
∴OB1=2,B1B2=3,B2H=t,
∴A3的坐标为(5+t,t),
把A3(5+t,t)代入y=
x+
得
(5+t)+
=t,解得t=
,
即点A3的纵坐标为(
)2,
同理可得点A4的纵坐标为(
)3,
所以点An的纵坐标为(
)n-1.
故选A.
 解:把A1(1,1),A2(
解:把A1(1,1),A2(| 7 |
| 2 |
| 3 |
| 2 |
|
|
所以一次函数解析式为y=
| 1 |
| 5 |
| 4 |
| 5 |
作A1C⊥x轴于C,A2D⊥x轴于D,A3H⊥x轴于H,如图,
则A1C=1,A2D=
| 3 |
| 2 |
∵△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,
∴OB1=2,B1B2=3,B2H=t,
∴A3的坐标为(5+t,t),
把A3(5+t,t)代入y=
| 1 |
| 5 |
| 4 |
| 5 |
| 1 |
| 5 |
| 4 |
| 5 |
| 9 |
| 4 |
即点A3的纵坐标为(
| 3 |
| 2 |
同理可得点A4的纵坐标为(
| 3 |
| 2 |
所以点An的纵坐标为(
| 3 |
| 2 |
故选A.
点评:本题考查了一次函数图象上点的坐标特征:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线;直线上任意一点的坐标都满足函数关系式y=kx+b.也考查了等腰直角三角形的性质.

练习册系列答案
相关题目
下列因式分解正确的是( )
| A、x3-x=x(x2-1) |
| B、(x-2)2=x2-4x+4 |
| C、-x2-4=-(x-2)(x+2) |
| D、x2+3x-4=(x-1)(x+4) |
 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于D,若CD=
如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于D,若CD=| 1 |
| 2 |
| A、6 | B、12 | C、18 | D、24 |
不等式2x>-3的最小整数解是( )
| A、-1 | B、0 | C、2 | D、3 |
下列四张扑克牌图案中,是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
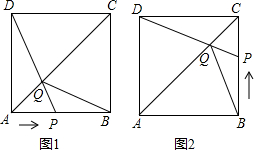 如图,在边长为1的正方形ABCD中,动点P从点A出发,沿着折线A→B→C的路线向终点C运动,连结DP交AC于点Q,连结BQ.
如图,在边长为1的正方形ABCD中,动点P从点A出发,沿着折线A→B→C的路线向终点C运动,连结DP交AC于点Q,连结BQ.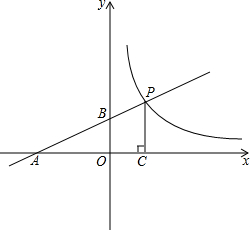 如图,直线
如图,直线