题目内容
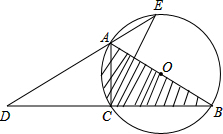 如图,AB为⊙O的直径,点C在⊙O上,延长BC至D,使得DC=CB,延长DA与⊙O交于点E,连接AC,CE.
如图,AB为⊙O的直径,点C在⊙O上,延长BC至D,使得DC=CB,延长DA与⊙O交于点E,连接AC,CE.(1)求证:∠D=∠E;
(2)若AB=4,
 |
| AC |
| 2 |
| 3 |
考点:扇形面积的计算,等腰三角形的判定与性质,勾股定理,圆周角定理
专题:
分析:(1)首先证明AD=AB,这是解决问题的关键;进而得到∠D=∠B;而∠B=∠E,即可解决问题.
(2)如图,作辅助线;先求出∠AOC=60°,进而求出∠B=30°;运用直角三角形的性质求出OF、BC的长,借助扇形的面积公式、直角三角形的面积公式即可解决问题.
(2)如图,作辅助线;先求出∠AOC=60°,进而求出∠B=30°;运用直角三角形的性质求出OF、BC的长,借助扇形的面积公式、直角三角形的面积公式即可解决问题.
解答:解:(1)∵AB是圆O直径,
∴AC⊥BD;
又∵DC=BC,
∴AC⊥BD,且平分BD,
∴AD=AB,
∴∠D=∠B;
∵∠B=∠E
∴∠D=∠E.
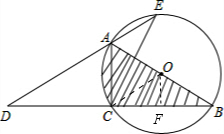 (2)如图,连接OC,过点O作OF⊥BC于点F.
(2)如图,连接OC,过点O作OF⊥BC于点F.
设∠AOC=α度,由弧长公式得:
=
,
∴α=60,即∠AOC=60°;
∵OB=OC,
∴∠OBC=∠OCB,而∠AOC=∠OBC+∠OCB,
∴∠B=30°,AC=
AB=2;OF=
OB=1;
∵cos30°=
,
∴BC=2
;
S阴影=S扇形AOC+S△BOC
=
×
π×2+
×2
×1
=
+
.
∴AC⊥BD;
又∵DC=BC,
∴AC⊥BD,且平分BD,
∴AD=AB,
∴∠D=∠B;
∵∠B=∠E
∴∠D=∠E.
 (2)如图,连接OC,过点O作OF⊥BC于点F.
(2)如图,连接OC,过点O作OF⊥BC于点F.设∠AOC=α度,由弧长公式得:
| 2απ |
| 180 |
| 2π |
| 3 |
∴α=60,即∠AOC=60°;
∵OB=OC,
∴∠OBC=∠OCB,而∠AOC=∠OBC+∠OCB,
∴∠B=30°,AC=
| 1 |
| 2 |
| 1 |
| 2 |
∵cos30°=
| BC |
| AB |
∴BC=2
| 3 |
S阴影=S扇形AOC+S△BOC
=
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
=
| 2π |
| 3 |
| 3 |
点评:该题主要考查了线段垂直平分线的性质、等腰三角形的判定及其性质、直角三角形的性质、扇形的面积公式等几何知识点的应用问题;解题的关键是灵活运用有关定理来分析、解答.

练习册系列答案
相关题目
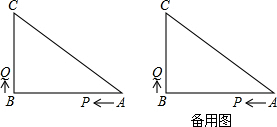 到达点A时,P、Q两点同时停止运动,它们同时出发,设出发的时间为t秒.
到达点A时,P、Q两点同时停止运动,它们同时出发,设出发的时间为t秒.