题目内容
已知x=2+
，y=2-
．
（1）求x2-4x的值，xy的值；
（2）求（x3-4x2+
）（y3-4y2+
）的值．
| 3 |
| 3 |
（1）求x2-4x的值，xy的值；
（2）求（x3-4x2+
| 1 |
| y |
| 1 |
| x |
考点：二次根式的化简求值
专题：
分析：（1）x2-4x=x（x-4）代入求解即可；
把x、y的值代入xy即可求得代数式的值；
（2）把x、y的值代入代数式，根据xy=1，以及x=
即可求解．
把x、y的值代入xy即可求得代数式的值；
（2）把x、y的值代入代数式，根据xy=1，以及x=
| 1 |
| y |
解答：解：（1）x2-4x=x（x-4）=（2+
）（
-2）=3-4=-1；
xy=（2+
）（2-
）-4-3=1；
（2）原式=【（2+
）3-4（2+
）2+
】【（2-
）3-4（2-
）2+
】
=【（2+
）2（2+
-4）+2+
】【（2-
）2（2-
-4）+2-
】
=【（2+
）2（
-2）+2+
】【-（2-
）2（2+
）+2-
】
=【-（2+
）+2+
】【-（2-
）+2-
】
=（-4+2
）×0
=0．
| 3 |
| 3 |
xy=（2+
| 3 |
| 3 |
（2）原式=【（2+
| 3 |
| 3 |
| 1 | ||
2-
|
| 3 |
| 3 |
| 1 | ||
2+
|
=【（2+
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
=【（2+
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
=【-（2+
| 3 |
| 3 |
| 3 |
| 3 |
=（-4+2
| 3 |
=0．
点评：本题考查了代数式的化简求值，理解（2+
）（2-
）=1是解决本题的关键．
| 3 |
| 3 |
练习册系列答案
相关题目
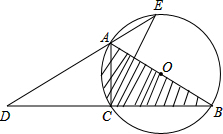如图，AB为⊙O的直径，点C在⊙O上，延长BC至D，使得DC=CB，延长DA与⊙O交于点E，连接AC，CE．