题目内容
如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿线段AB向点B运动,且速度为每秒1cm,点Q从点B开始沿折线B-C-A运动,且速度为每秒2cm,当点Q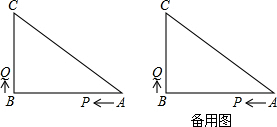 到达点A时,P、Q两点同时停止运动,它们同时出发,设出发的时间为t秒.
到达点A时,P、Q两点同时停止运动,它们同时出发,设出发的时间为t秒.
(1)当点Q在边BC上运动时,出发几秒钟,△PQB能形成等腰三角形?
(2)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间(只要直接写出答案).
 到达点A时,P、Q两点同时停止运动,它们同时出发,设出发的时间为t秒.
到达点A时,P、Q两点同时停止运动,它们同时出发,设出发的时间为t秒.(1)当点Q在边BC上运动时,出发几秒钟,△PQB能形成等腰三角形?
(2)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间(只要直接写出答案).
考点:等腰三角形的判定与性质,勾股定理
专题:
分析:(1)根据题意可知AP=t,BQ=2t,根据条件可得到BP=BQ,得到关于t的方程可求得t;
(2)分BQ=BC,CQ=BC和BQ=CQ三种情况分别讨论得到关于t的方程,求出t即可.
(2)分BQ=BC,CQ=BC和BQ=CQ三种情况分别讨论得到关于t的方程,求出t即可.
解答:解:(1)由题意可知AP=t,BQ=2t,
∵AB=8,
∴BP=AB-AP=8-t,
当△PQB为等腰三角形时,则有BP=BQ,
即8-t=2t,解得t=
,
∴出发
秒后△PQB能形成等腰三角形;
(2)在△ABC中,由勾股定理可求得AC=10,
当点Q在AC上时,AQ=BC+AC-2t=16-2t,所以CQ=AC-AQ=10-(16-2t)=2t-6,
当BQ=BC=6时,如图1,过B作BD⊥AC,则CD=
CQ=t-3,在Rt△ABC中,可求得BD=
,
在Rt△BCD中,由勾股定理可得BC2=BD2+CD2,即62=(
)2+(t-3)2,解得t=
或t=-
<0(舍去);
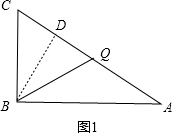
当CQ=BC=6时,则2t-6=6,解得t=6,
当CQ=BQ时,则∠C=∠QBC,
∴∠C+∠A=∠CBQ+∠QBA,
∴∠A=∠QBA,
∴QB=QA,
∴CQ=
AC=5,即2t-6=5,解得t=5.5,
综上可知当△BCQ为等腰三角形时,t=
或t=6或t=5.5.
∵AB=8,
∴BP=AB-AP=8-t,
当△PQB为等腰三角形时,则有BP=BQ,
即8-t=2t,解得t=
| 8 |
| 3 |
∴出发
| 8 |
| 3 |
(2)在△ABC中,由勾股定理可求得AC=10,
当点Q在AC上时,AQ=BC+AC-2t=16-2t,所以CQ=AC-AQ=10-(16-2t)=2t-6,
当BQ=BC=6时,如图1,过B作BD⊥AC,则CD=
| 1 |
| 2 |
| 24 |
| 5 |
在Rt△BCD中,由勾股定理可得BC2=BD2+CD2,即62=(
| 24 |
| 5 |
| 33 |
| 5 |
| 3 |
| 5 |

当CQ=BC=6时,则2t-6=6,解得t=6,
当CQ=BQ时,则∠C=∠QBC,
∴∠C+∠A=∠CBQ+∠QBA,
∴∠A=∠QBA,
∴QB=QA,
∴CQ=
| 1 |
| 2 |
综上可知当△BCQ为等腰三角形时,t=
| 33 |
| 5 |
点评:本题主要考查等腰三角形的判定和性质,掌握等腰三角形的两腰相等是解题的关键,利用t表示出线段的长度,化动为静是解决这类问题的常用思路.

练习册系列答案
相关题目
下列函数是二次函数的是( )
| A、y=8x2+1 | ||
| B、y=8x+1 | ||
| C、y=8x | ||
D、y=
|
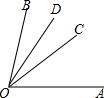 如图,已知OC是∠AOB的平分线,∠AOD比∠BOD大40°,求∠COD的度数.
如图,已知OC是∠AOB的平分线,∠AOD比∠BOD大40°,求∠COD的度数.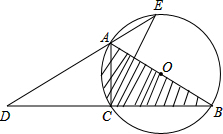 如图,AB为⊙O的直径,点C在⊙O上,延长BC至D,使得DC=CB,延长DA与⊙O交于点E,连接AC,CE.
如图,AB为⊙O的直径,点C在⊙O上,延长BC至D,使得DC=CB,延长DA与⊙O交于点E,连接AC,CE.
 把1000以内从1开始的自然数排列成右图,用正方形框往上下左右相邻的4个数.
把1000以内从1开始的自然数排列成右图,用正方形框往上下左右相邻的4个数.