题目内容
19.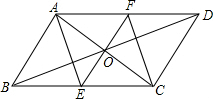 如图,在?ABCD中,EF经过对角线的交点O,且EF⊥AC分别交CD、AB于点E,F,试说明四边形AECF是菱形.
如图,在?ABCD中,EF经过对角线的交点O,且EF⊥AC分别交CD、AB于点E,F,试说明四边形AECF是菱形.
分析 由ASA证明△AOF≌△COE,得出对应边相等EO=FO,证出四边形AECF为平行四边形,再由对角线互相垂直,即可得出结论.
解答 证明:∵四边形ABCD是平行四边形,
∴AO=CO,AF∥EC.
∴∠FAC=∠ECA.
在△AOF与△COE中,$\left\{\begin{array}{l}{∠FAC=∠ECA}&{\;}\\{AO=CO}&{\;}\\{∠AOF=∠COE}&{\;}\end{array}\right.$,
∴△AOF≌△COE(ASA).
∴EO=FO,
∴四边形AECF为平行四边形,
又∵EF⊥AC,
∴四边形AECF为菱形.
点评 本题考查了菱形的判定、平行四边形的判定与性质、全等三角形的判定与性质;熟练掌握平行四边形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
20.?ABCD的对角线相交于点O,下列结论错误的是( )
| A. | ?ABCD是中心对称图形 | B. | △AOB与△BOC的面积相等 | ||
| C. | △AOB≌△COD | D. | △AOB≌△BOC |
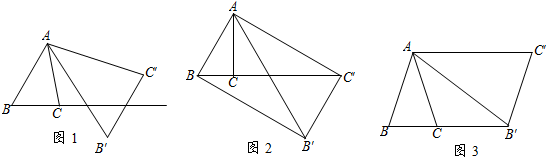
 如图,在菱形ABCD中,点P在对角线BD上,CP的延长线交AD于点E,交BA的延长线于点F,求证:△APE∽△FPA.
如图,在菱形ABCD中,点P在对角线BD上,CP的延长线交AD于点E,交BA的延长线于点F,求证:△APE∽△FPA.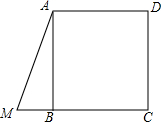 如图,正方形ABCD,点M是线段CB延长线一点,连结AM,AB=a,BM=b.
如图,正方形ABCD,点M是线段CB延长线一点,连结AM,AB=a,BM=b.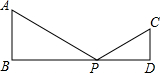 如图,AB⊥BD,CD⊥BD,AB=6cm,CD=4cm,BD=14cm,点P在BD上由点B向点D方向移动,当点P移到离点B多远时,△APB和△CPD相似?
如图,AB⊥BD,CD⊥BD,AB=6cm,CD=4cm,BD=14cm,点P在BD上由点B向点D方向移动,当点P移到离点B多远时,△APB和△CPD相似?