题目内容
4.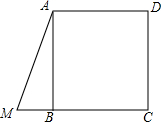 如图,正方形ABCD,点M是线段CB延长线一点,连结AM,AB=a,BM=b.
如图,正方形ABCD,点M是线段CB延长线一点,连结AM,AB=a,BM=b.(1)将线段AM沿着射线AD运动,使得点A与点D重合,用代数式表示线段AM扫过的平面部分的面积.
(2)将三角形ABM绕着点A旋转,使得AB与AD重合,点M落在点N,连结MN,用代数式表示三角形CMN的面积.
(3)将三角形ABM顺时针旋转,使旋转后的三角形有一边与正方形的一边完全重合(第(2)小题的情况除外),请在如图中画出符合条件的3种情况,并写出相应的旋转中心和旋转角.
分析 (1)根据平移的性质和平行四边形的面积计算即可;
(2)根据三角形的面积计算即可;
(3)根据旋转的性质画出图形得出旋转中心和角度即可.
解答 解:(1)AD•DC=a2,
答:线段AM扫过的平面部分的面积为a2,;
(2)$\frac{1}{2}MC•NC=\frac{1}{2}(a+b)(a-b)=\frac{1}{2}{a}^{2}-\frac{1}{2}{b}^{2}$,
答:三角形CMN的面积为$\frac{1}{2}{a}^{2}-\frac{1}{2}{b}^{2}$;
(3)如图1,旋转中心:AB边的中点为O,顺时针180°,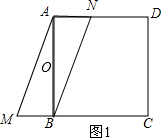 ;
;
如图2,旋转中心:点B;顺时针旋转90°,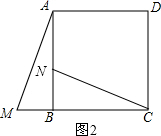 ;
;
如图3,旋转中心:正方形对角线交点O;顺时针旋转90°,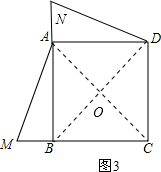 .
.
点评 本题考查了旋转的性质,关键是根据旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角解答.

练习册系列答案
相关题目
 如图,直线y=x+3分别交x,y轴于点D,C,点B在x轴上,OB=OC,过点B作直线m∥CD.点P、Q分别为直线m和直线CD上的动点,且点P在x轴的上方,满足∠POQ=45°
如图,直线y=x+3分别交x,y轴于点D,C,点B在x轴上,OB=OC,过点B作直线m∥CD.点P、Q分别为直线m和直线CD上的动点,且点P在x轴的上方,满足∠POQ=45°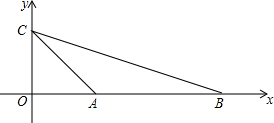 如图,已知A(1,0)、C(0,1)、B(m,0)且m>1,在平面内求一点P,使得以A、B、C、P为顶点的四边形是平行四边形,则点P的坐标为(m-1,1)或(1-m,1)或(m+1,-1).
如图,已知A(1,0)、C(0,1)、B(m,0)且m>1,在平面内求一点P,使得以A、B、C、P为顶点的四边形是平行四边形,则点P的坐标为(m-1,1)或(1-m,1)或(m+1,-1).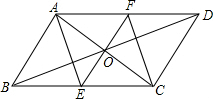 如图,在?ABCD中,EF经过对角线的交点O,且EF⊥AC分别交CD、AB于点E,F,试说明四边形AECF是菱形.
如图,在?ABCD中,EF经过对角线的交点O,且EF⊥AC分别交CD、AB于点E,F,试说明四边形AECF是菱形.