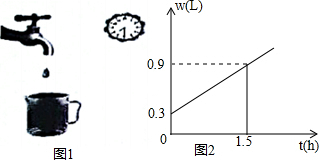
题目内容
1．用配方法求下列函数的顶点坐标（1）y=x2+2x-3
（2）y=（x-1）（x+2）
分析 根据配方法的一般步骤把一般式化为顶点式，根据二次函数的性质求出顶点坐标即可．
解答 解：（1）y=x2+2x-3=（x+1）2-4，
则抛物线的顶点坐标为（-1，-4）；
（2）y=（x-1）（x+2）=x2+x-2=（x+$\frac{1}{2}$）2-2$\frac{1}{4}$．
则抛物线的顶点坐标为（-$\frac{1}{2}$，-2$\frac{1}{4}$）．
点评 本题考查的是二次函数的一般式化为顶点式和二次函数的性质，正确运用配方法把一般式化为顶点式是解题的关键．
练习册系列答案
相关题目
11．下列运算正确的是（ ）
| A． | （3x2）3=9x6 | B． | a6÷a2=a3 | C． | （a+b）2=a2+b2 | D． | （a-b）（a+b）=a2-b2 |
在正方形ABCD处，以BC为边作一个等边三角形△BCE，则∠DCE=150°．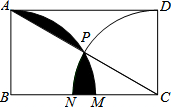
如图，在矩形ABCD中，AB=1，分别以点B、C为圆心，1为半径画弧，与BC边分别交于点M、N，且与对角线AC交于同一点P，则图中阴影部分的面积为$\frac{π}{3}$-$\frac{\sqrt{3}}{2}$．
6．下列运算正确的是（ ）
| A． | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B． | a6÷a2=a3 | C． | （π-3）0=1 | D． | （2a）3=6a3 |
