题目内容
15.声音在空气中传播的速度y(m/s)与气温x(℃)(0≤x≤25)之间的关系如下表:| 气温x/℃ | 0 | 5 | 10 | 15 | 20 |
| 声速y/m•s-1 | 331 | 334 | 337 | 340 | 343 |
(2)画出函数的图象;
(3)气温在22℃时,有人看到烟花燃放5秒后,才听到声响,那么此人距燃放烟花的所在的地方有1721m.
分析 (1)由表中的数据可知,温度每升高5℃,声速就提高3米/秒,所以y是x的一次函数,利用待定系数法即可求出该函数解析式;
(2)根据解析式画出图象即可;
(3)令x=22,求出此时的声速y,然后利用路程=速度×时间即可求出该距离.
解答 解:(1)根据表中数据画图象可知y与x成一次函数关系,
故设y=kx+b,取两点(0,331),(5,334)代入关系式得
$\left\{\begin{array}{l}{331=b}\\{334=5k+b}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{3}{5}}\\{b=331}\end{array}\right.$,
∴函数关系式为y=$\frac{3}{5}$x+331.
(2)图象如图:
(3)把x=22代入y=$\frac{3}{5}$x+331.
得y=$\frac{3}{5}$×22+331=334$\frac{1}{5}$,且334$\frac{1}{5}$×5=1721m.
∵光速非常快,传播时间可以忽略,
∴此人与燃放烟花的所在地相距约1721m.
故答案为:y=$\frac{3}{5}$x+331;1721.
点评 此题考查一次函数的应用,本题需仔细分析表中的数据,利用待定系数法即可解决问题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
5.下列运算正确的是( )
| A. | a3•a2=a6 | B. | $\sqrt{9}$=3 | C. | (a2)3=a5 | D. | 4a-2a=2 |
6.下列运算正确的是( )
| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | a6÷a2=a3 | C. | (π-3)0=1 | D. | (2a)3=6a3 |
3.下列运算结果为负数的是( )
| A. | -(-2) | B. | (-2)2 | C. | |-2| | D. | (-2)3 |
4.下列计算正确的是( )
| A. | a4÷a3=1 | B. | a4+a3=a7 | C. | (2a3)4=8a12 | D. | a4•a3=a7 |
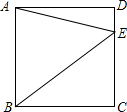 如图,点E在正方形ABCD的边CD上,若△ABE的面积为8,DE=1,则线段BE=5.
如图,点E在正方形ABCD的边CD上,若△ABE的面积为8,DE=1,则线段BE=5.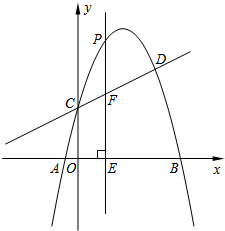 如图,抛物线y=-x2+bx+c与直线y=$\frac{1}{2}$x+2交于C,D两点,其中点C在y轴上,点D的横坐标为3,点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
如图,抛物线y=-x2+bx+c与直线y=$\frac{1}{2}$x+2交于C,D两点,其中点C在y轴上,点D的横坐标为3,点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.