题目内容
17.解方程:($\sqrt{2}$+1)x+($\sqrt{2}$-1)x=6.分析 原方程两边同乘($\sqrt{2}$+1)x整理得:($\sqrt{2}$+1)2x-6($\sqrt{2}$+1)x+1=0,设($\sqrt{2}$+1)x=y,则化为y2-6y+1=0,用公式法解方程求得y的值,再把y=-2和2分别代入($\sqrt{2}$+1)x=y,即可确定原方程的解.
解答 解:原方程两边同乘($\sqrt{2}$+1)x整理得:($\sqrt{2}$+1)2x-6($\sqrt{2}$+1)x+1=0,
设($\sqrt{2}$+1)x=y,则y2-6y+1=0,
∵b2-4ac=36-4=32>0,
∴y=$\frac{6±\sqrt{32}}{2}$,
∴y1=3+2$\sqrt{2}$,y2=3-2$\sqrt{2}$,
当($\sqrt{2}$+1)x=3+2$\sqrt{2}$时,x=2,
当($\sqrt{2}$+1)x=3-2$\sqrt{2}$时,x=-2,
∴原方程的解为:x1=2,x2=-2.
点评 本题考查了换元法解一元二次方程:我们常用的是整体换元法,是在已知或者未知中,某个代数式几次出现,而用一个字母来代替它从而简化问题,当然有时候要通过变形才能发现.把一些形式复杂的方程通过换元的方法变成简单方程.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
5.画△ABC的边AC上的高,下列画法中正确的是 ( )
| A. |  | B. |  | C. |  | D. |  |
3.若关于x的方程$\frac{{x}^{2}-bx}{ax-c}$=$\frac{m-1}{m+1}$有绝对值相同,符号相反的两个根,则m的值应为( )
| A. | c | B. | $\frac{1}{c}$ | C. | $\frac{a-b}{a+b}$ | D. | $\frac{a+b}{a-b}$ |
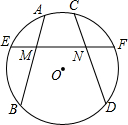 如图,弦AB,CD交EF于M,N,且ME=NF,∠AMN=∠CNM,求证:AB=CD.
如图,弦AB,CD交EF于M,N,且ME=NF,∠AMN=∠CNM,求证:AB=CD.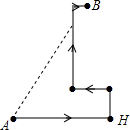 假期中,王强和同学们到某海岛上去玩探宝旅游,按照探宝图(如图),他们在A点登陆后先往东走8$\sqrt{3}$千米到H点,又往北走2$\sqrt{3}$千米,遇到障碍后又往西走了3$\sqrt{3}$千米,再折向北走了6$\sqrt{3}$千米处往东一拐,再走了$\sqrt{3}$千米就找到宝藏埋藏点B,问:他们共走了多少千米?
假期中,王强和同学们到某海岛上去玩探宝旅游,按照探宝图(如图),他们在A点登陆后先往东走8$\sqrt{3}$千米到H点,又往北走2$\sqrt{3}$千米,遇到障碍后又往西走了3$\sqrt{3}$千米,再折向北走了6$\sqrt{3}$千米处往东一拐,再走了$\sqrt{3}$千米就找到宝藏埋藏点B,问:他们共走了多少千米?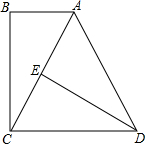 如图,已知AB∥CD,BC⊥AB,∠CAD=60°,且AD=DC,E是AC的中点,求证:BC=ED.
如图,已知AB∥CD,BC⊥AB,∠CAD=60°,且AD=DC,E是AC的中点,求证:BC=ED. 如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数.
如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数. 如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连接AD、AO、AE、BO、CO,△ADE的周长为6,△OBC的周长为16,求AO的长.
如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连接AD、AO、AE、BO、CO,△ADE的周长为6,△OBC的周长为16,求AO的长.