题目内容
2.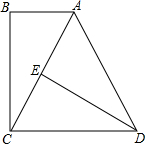 如图,已知AB∥CD,BC⊥AB,∠CAD=60°,且AD=DC,E是AC的中点,求证:BC=ED.
如图,已知AB∥CD,BC⊥AB,∠CAD=60°,且AD=DC,E是AC的中点,求证:BC=ED.
分析 根据等边三角形的判定与性质得出DE⊥AC,∠BAC=∠ACD=60°,进而求出△ADE≌△ACB(AAS),求出即可.
解答  证明:∵∠CAD=60°且AD=DC,
证明:∵∠CAD=60°且AD=DC,
∴△ACD是等边三角形,
∴AC=AD=CD,∠ACD=60°,
∵E是AC的中点,
∴DE⊥AC,
∵AB∥CD,
∴∠BAC=∠ACD=60°,
∴在△ADE和△ACB中
$\left\{\begin{array}{l}{∠DEA=∠CBA}\\{∠EAD=∠BAC}\\{AD=AC}\end{array}\right.$,
∴△ADE≌△ACB(AAS),
∴BC=ED.
点评 此题主要考查了全等三角形的判定与性质以及等边三角形的判定与性质,得出△ADE≌△ACB是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.某珠宝店失窃,甲、乙、丙、丁四人涉嫌被拘审,四人的口供如下:甲:作案的是丙;乙:丁是作案者;丙:如果我作案,那么丁是主犯;丁:作案的不是我.如果四人口供中只有一个是假的,那么以下判断正确的是( )
| A. | 说假话的是甲,作案的是乙 | B. | 说假话的是丁,作案的是丙和丁 | ||
| C. | 假话的是乙,作案的是丙 | D. | 说假话的是丙,作案的是丙 |
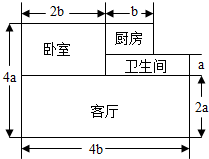 李叔叔买了一套新房,其结构如图(单位:m),他打算除卧室外,其余部分铺地砖.
李叔叔买了一套新房,其结构如图(单位:m),他打算除卧室外,其余部分铺地砖. 如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AC,∠BAC=120°,BC=12cm,则DE=3cm.
如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AC,∠BAC=120°,BC=12cm,则DE=3cm.